
Нередко перед людьми встает вопрос, как складывать дроби. Ведь не стоит скрывать, что многое из того, что проходят в школе, мы проходили мимо. А тут вдруг ребенку-школьнику позарез нужна ваша помощь в решении подобных задач. Но не отчаивайтесь! При желании с такого рода задачами можно справиться на раз-два!
Когда вы будете учиться сложению дробных частей целого, необходимо учесть, что существуют разные случаи и алгоритм действий в них различен.
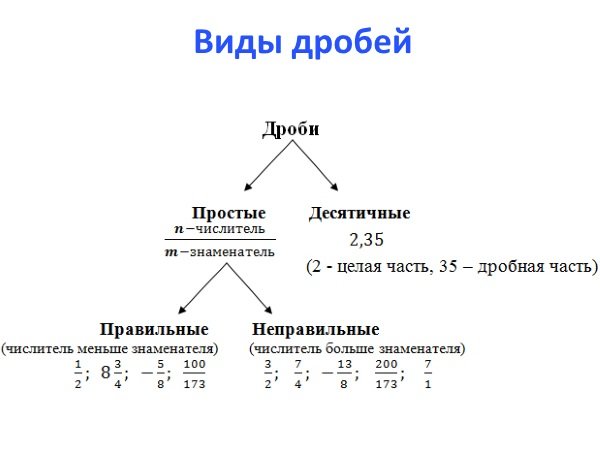
Для начала немного теории
Как мы знаем, нецелое число, то есть дробное, состоит из одной или нескольких частей единицы, например: ½, ¾, 0,5, 2 ½.
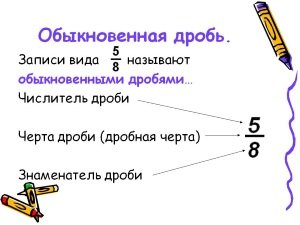
Обыкновенные дроби записываются как m/n, где косая черта обозначает деление. Число, которое делят (m), называют числителем, а число, на которое делят (n), — знаменателем. В результате деления выходит частное.

До запятой записывается целая часть, после же — делимое. Рассмотрим конкретный пример.
Необходимо преобразовать 22/10 в десятичную. Записываем делимое: в нашем случае 22. Теперь нам нужно определить, где именно поставить запятую.
Для этого считаем, сколько есть нулей в делящем числовом значении. У нас один ноль, поэтому отсчитываем один знак справа налево и ставим «точку с хвостом». У нас выходит 2,2.
Теперь, когда мы разобрались, чем различаются обычные и десятичные дроби, можно перейти к сложению.
Разберемся с обыкновенными
Рассмотрим конкретный пример: сложим 1/3 и 2/3.
1/3 + 2/3 = (1 + 2)/3 = 3/3.
Но это не все. Как складывать дроби с одинаковыми знаменателями, мы разобрались, но перед тем, как записать ответ, стоит посмотреть, нельзя ли эту дробную часть «сократить». Как это сделать?
Если делимое больше делителя, то вычитаем из верхнего числового значения нижнее до тех пор, пока оно не станет меньше. Количество вычитаний — это количество целых единиц. В нашем случае:
3 — 3 = 0, в итоге в ответ записываем 1.
Теперь попробуем сложить две дроби с разными делителями. Это немного сложнее, необходимо соблюдать алгоритм действий.
Итак, чтобы сложить дроби с разными знаменателями, нужно привести дробные числовые значения к общему знаменателю. Разберем на примере.
1/12 + 3/10 =
Находим наименьшее общее кратное числовых значений под чертой. В данном случае, 60. После этого находим дополнительные множители для каждого из них: для этого достаточно разделить наименьшее общее кратное на каждый множитель.
В нашем случае, дополнительным множителем к первому числу будет 60 : 12 = 5, а ко второму — 60 : 10 = 6.
Теперь умножаем и делимое, и делитель обоих слагаемых на их дополнительные множители. Теперь, когда у нас получились дроби с одинаковыми знаменателями, воспользуемся вышеописанным алгоритмом.
5/60 + 18/60 = 23/60.
После того как мы научились складывать дроби с разными знаменателями, перейдем к самому сложному. Готовьтесь, перед нами смешанные дроби. Смешанными называют те числа, в которых есть и целая, и дробная части.
Разобраться, как складывать смешанные числа, достаточно просто: необходимо лишь для начала сложить целые, а потом по алгоритму выше сложить 2 нецелые.
Вместе одолеем десятичные
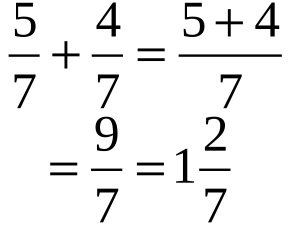
Если они имеют разное количество знаков в нецелой части, необходимо приписывать к той, которая имеет меньше знаков, нули до тех пор, пока знаки после запятой в обеих не уравняются.
Например, попробуем провести операцию сложения 22,1 и 0,31.
22,10
+ 0,31
________
22,41
Есть и другой способ: представить десятичную дробь в виде обычной. Как мы уже говорили, количество знаков после запятой является количеством нулей в делителе. Таким образом, получаем:
221/10 + 31/100 = 2241/100 = 22 41/100.
Как видите, все совсем не так страшно, как кажется на первый взгляд.
Главное — начать, а дальше дело пойдет в гору!

