10.3. Приемы оценки прогностической ценности методик

10.3. Приемы оценки прогностической ценности методик

Прогностическая ценность (информативность, прогностичность) как отдельных методик, так и интегрального показателя профессиональной пригодности может определяться в зависимости от целей выявления профпригодности (отбор, подбор, экспертиза и т. д.) по одному из критериев профессиональной успеваемости, эффективности реальной деятельности, по их совокупности или по ведущему критерию (по оценке профессиональных способностей).

При сопоставлении указанных параметров большое значение имеет выбор соответствующих математико-статистических моделей оценки различий и связи между признаками. В практике психологического отбора летчиков себя оправдали такие методы, как анализ альтернативных признаков, критерии величины и достоверности различий, корреляционный анализ и др.

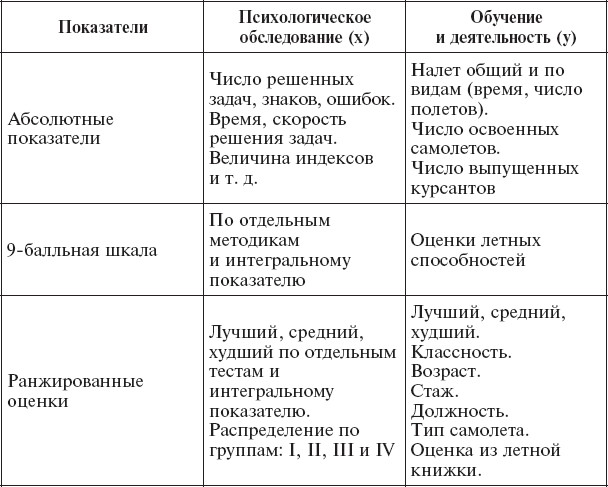
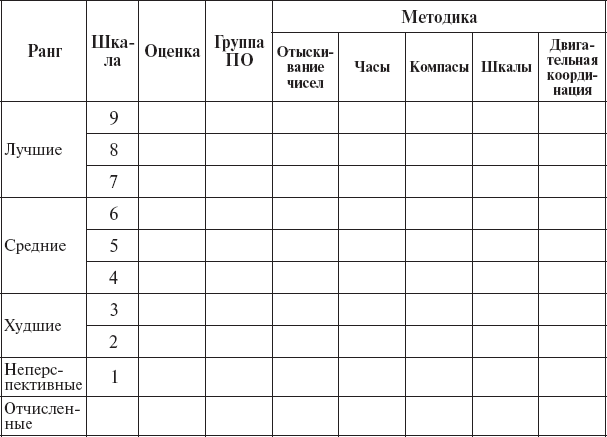
Основные критерии, по которым можно проводить сравнение результатов экспериментально-психологического обследования с успешностью летного обучения и деятельности для определения прогностической валидности методик психологического отбора, приведены в таблице 2.

Анализ альтернативных признаков. Определяя основные показатели профпригодности и успешности профессионального обучения, приходится иметь дело с изменчивостью качественных признаков, которые в вариационные ряды не распределяются, а рассматриваются как противопоставляемые друг другу состояния. Например, из 700 кандидатов в IV группу психологического отбора вошло 50 человек. Анализируя данные, мы противопоставляем эту группу оставшимся 650 кандидатам. В такой альтернативной форме могут рассматриваться как качественные, так и количественные признаки сравниваемых явлений.

Таблица 2.

Основные показатели оценки результатов экспериментально-психологического обследования и профессиональной деятельности

Альтернативные признаки выражаются в абсолютных значениях частот, с которыми они встречаются в данной совокупности, а также в долях единицы или в процентах от общего числа наблюдений. Например, в отношении обследованных 700 кандидатов можно сказать, что среди них IV группа составляет 7 %.

Основным альтернативным признаком для оценки эффективности психологического отбора в целом следует считать относительное распределение по группам и баллам учащихся, отчисленных по различным причинам и отдельно по профессиональной неуспеваемости (табл. 3).

Таблица 3

Количество курсантов, отчисленных по летной неуспеваемости, по группам, по 9-балльной шкале психологического отбора и курсам обучения

Аналогично можно проанализировать другие причины отчислений из училища (теоретическая неуспеваемость, медицинское несоответствие, нежелание учиться, недисциплинированность).

Прогностическая эффективность отдельных методик и интегрального показателя психологического отбора могут быть также определены по формуле:

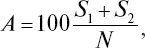
где А – общий процент оправдавшихся прогнозов; S₁, S₂ – число положительных и отрицательных прогнозов, которые оправдались; N – общее число кандидатов.

Критерии, по которым оценивается эффективность психологического отбора в отношении успешности освоения программы профессионального обучения (исключая отчисленных), приведены в таблице 4.

Таблица 4

Распределение средних величин ранговых порядков, оценок летных способностей, числа полетов по группам, 9-балльной шкале психологического отбора и курсам обучения (1–4)

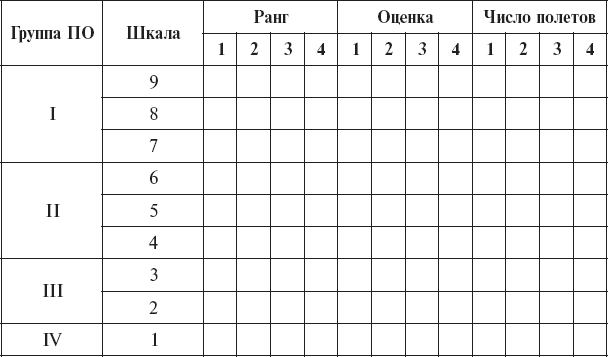
Имея ранжированные критерии успешности летного обучения (оценка летных способностей по 9-балльной шкале и ранговые порядки), необходимо через них проанализировать прогностичность критериев психологического отбора (табл. 5).

Для правильной оценки полученных средних величин критериев психологического отбора при сопоставлении их с критериями успешности обучения необходимым является определение величины и достоверности различных сравниваемых параметров.

Критерии величины и достоверности различий. Прогностическая валидность методик в зависимости от характеристик оценок используемых внешних критериев и теста может определяться также путем выделения из всего контингента двух групп: а) заведомо хороших специалистов (лучших); б) бесспорно плохих (худших) или отчисленных по неспособности к обучению. Результаты психологического обследования по методике или интегральному показателю этих групп составляют два вариационных ряда, и по различиям между ними определяется прогностическая валидность. Если ряды окажутся статистически неразличимы, то данная методика не содержит сведений для дифференциальной диагностики пригодных и непригодных специалистов, то есть ее информативность мала. Чем больше степень различия, тем выше информативность методики. Сравнение вариационных рядов можно проводить с помощью различных методов.

Таблица 5

Распределение средних величин результатов психологического отбора по 9-балльной шкале летных способностей и ранговым порядкам при освоении учебного (учебно-боевого) самолета

В большинстве случаев, когда распределение вариант в изучаемых совокупностях достаточно близко к нормальному виду, для сравнения средних значений применяется критерий Стьюдента (1), являющийся величиной безразмерной.

Уровень значимости различий P между сравниваемыми средними находится по t в специальной таблице. P зависит от числа степеней свободы (К) или объема выборки (N) и величины t. В практике статистической обработки результатов исследований принято использовать три уровня значимости: P₁ = 95 %, P₂ = 99 %, P₃ = 99,9 %. Величина уровня значимости устанавливается самим исследователем в зависимости от степени точности, с какой проводится исследование, и ответственности выводов, вытекающих из него. Обычно уровень значимости различий между сравниваемыми параметрами, равный 95 %, считается достаточно надежным. Однако в тех случаях, когда на основании проведенных исследований делаются широкие обобщения и выводы особенно строгие, принимаются (99 %) и 99,9 %-ные уровни. Например, когда исследователь приходит к выводу о необходимости включения новой методики в комплекс имеющихся тестов или о нецелесообразности приема для обучения определенной категории кандидатов в связи с высоким процентом отчислений и большими денежными затратами на их подготовку, то уровень значимости, конечно, должен быть очень высоким.

В случаях, когда необходимо проверить гипотезу при небольшой выборке и отсутствии нормального распределения, проверка значимости различий между сравниваемыми параметрами может быть осуществлена с помощью критериев, не требующих трудоемкого вычисления каких-либо статистических параметров, то есть непараметрических критериев различия. Кроме того, они весьма удобны для анализа таких исследований, где сравниваемые показатели выражаются не в конкретных (абсолютных) мерах измерения (количество полетов, время и т. п.), а шкалами порядка, баллами или рангами по изучаемому признаку.

Учитывая, что все методики и интегральный показатель психологического отбора, а также основные критерии успешности профессионального (летного) обучения выражаются именно в баллах и рангах, использование непараметрических критериев должно найти широкое применение.

Применяя непараметрические критерии различий, необходимо вначале использовать менее мощные (критерий Вилкоксона и критерий Розенбаума), но и менее трудоемкие, а при получении сомнительных результатов применить более мощные (критерии Ван дер Вардена, Колмогорова – Смирнова).

Для определения различий при помощи критерия Вилкоксона [141] следует расположить все данные в один упорядоченный ряд и проставить их ранги (R). Например, необходимо сравнить результаты психологического отбора по методике «Шкалы» у лучших (x) и худших (y) по летной подготовке на учебном самолете – соответственно 9 и 9 курсантов.

Располагаем баллы лучших и худших в упорядоченные ряды:

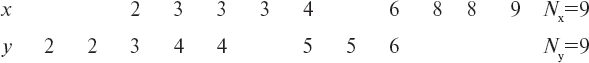
Далее, упорядоченные ряды необходимо проранжировать и подсчитать сумму рангов для каждого из рядов:

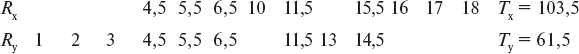
После подсчета находим в специальной таблице на пересечении N_x и N_y критическое значение T, которое сравнивается с меньшей из суммы T_x и T_y, и определяется уровень достоверности различий. В случае, когда меньшая из сумм превосходит критическое значение T, разница между сравниваемыми параметрами считается недостоверной или, наоборот, достоверной на 95 %-ном или более уровне значимости.

В разбираемом случае критическое значение T для N_x = 9 и N_y = 10 на уровне достоверности различий в 95 % равно 64, а в 99 % – 58. Анализируя прогностичность методики «Шкалы», можно отметить, что критическое значение T больше суммы T_y (меньшая из двух); 65 больше 61,5, а это свидетельствует о достоверности различий между лучшими и худшими по летной подготовке на уровне 95 % в выполнении ими данного теста.

Параметрические и непараметрические критерии можно использовать при определении достоверности различий между группами психологического отбора, интегральным баллом, баллами по отдельным методикам, с одной стороны, а с другой – различными категориями отчисленных студентов (курсантов), баллами профессиональных способностей, рангами, числом полетов, то есть практически между всеми критериями психологического отбора и успешности обучения.

Корреляционный анализ. При изучении взаимосвязи критериев психологического отбора с успешностью обучения и профессиональной деятельности можно заметить, что изменения первого признака соответствуют изменениям второго. В некоторых случаях зависимость проявляется очень сильно, однако такие однозначные или функциональные связи встречаются редко, особенно в психологических исследованиях, где числовой характеристике теста может соответствовать не одно определенное значение критерия профессиональной деятельности, а целый ряд их варьирующих значений.

В большинстве психолого-педагогических исследований связь между результатами обследования и успешностью обучения довольно часто и сильно нарушается различными привходящими факторами, поэтому она не всегда может быть четко установлена. В таких случаях зависимость между изучаемыми критериями носит характер, при котором каждому значению одной из переменных соответствует не какое-то конкретное значение, а определенная групповая средняя другой переменной.

Такая связь называется корреляционной (корреляция), а математический анализ связей, существующий между ними, составляет содержание корреляционного анализа.

В задачи корреляционного анализа при определении прогностической валидности методик входит измерение тесноты или степени сопряженности между варьирующими признаками, ее направления и формы, а также последующая оценка достоверности полученных показателей связи.

Корреляционную связь между изучаемыми признаками можно обнаружить с помощью ряда показателей. Решению вопроса о выборе наиболее адекватного метода помогает предварительное расположение в определенном порядке двух сопряженных рядов, позволяющее судить о наличии или отсутствии связи между ними. Более информативным является составление корреляционных матриц и графиков регрессии, дающих наглядное представление о форме и направлении корреляции, а также ее динамике.

При выборе того или иного показателя необходимо учесть, по каким признакам проводится корреляционный анализ (качественным или количественным), форму корреляционной зависимости (линейная или нелинейная) и возможность группирования изучаемых величин в вариационные ряды. Следует помнить, что корреляционный анализ служит инструментом только количественного выражения связей между варьирующими признаками и позволяет оценить достоверность корреляции. Поэтому, несмотря на большую ценность этого метода, его не следует переоценивать, а тем более подменять им профессиональный и психолого-педагогический анализ факторов.

При изучении связи между критериями психологического отбора и успешностью летного обучения целесообразно построение «корреляционной решетки» (табл. 6).

Таблица 6

Образец построения корреляционной решетки для 9-балльной шкалы

Частота вариант сопряженных видов – P_xy, занимая в таблице определенное положение, позволяет судить о наличии и направлении и частично о тесноте связи между баллами психологического отбора и баллами успешности летного обучения (варьирующими признаками) – x и y.

Если частоты P_xy располагаются преимущественно по диагонали с левого верхнего угла решетки к правому нижнему, как показано в нашем примере, – это указывает на положительную связь между признаками. При отсутствии корреляционной связи частоты распределяются по клеткам корреляционной решетки равномерно. О наличии отрицательной связи свидетельствует распределение частот в направлении от верхнего правого к нижнему левому углу. Это правомерно для тех случаев, когда баллы (классовые варианты) располагаются по возрастанию или убыванию (однонаправленно) слева направо сверху вниз.

После предварительного изучения (по характеру распределения частот в корреляционной решетке) тесноты и направления связи при определении необходимости дальнейшего анализа вычисляется коэффициент корреляции (r).

При изучении корреляции между критериями, выраженными в абсолютных величинах и с небольшим количеством сопоставляемых пар, техника вычисления r довольно проста. Например, необходимо изучить связь между результатами выполнения методики «Часы» (число ошибок) – x и количеством полетов на учебно-боевом самолете – y (табл. 7).

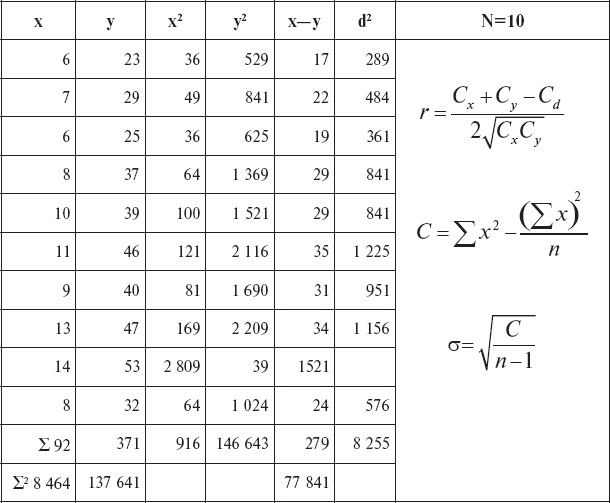
Для вычисления коэффициента корреляции необходимо еще определить величину дисперсии – С для x, y, d по формуле

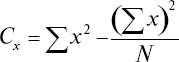
Подставляя значения из таблицы в формулу, находим: C_x = 69,6; C_y = 878,9; C_d = 470,9; r = 0,965. Устанавливаем достоверность полученного коэффициента корреляции:

Таблица 7

Вычисление коэффициента корреляции

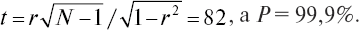
В данном случае коэффициент корреляции можно было вычислить не по абсолютным (числовым) значениям признаков, а по соответствующим рангам, которые имеет каждый курсант. Такой анализ взаимосвязи называется «показатель корреляции рангов» (табл. 8).

Показатель корреляции рангов несколько отличается от коэффициента корреляции, так как ранги не могут точно соответствовать равностоящим значениям количественных величин. Учитывая, что неточность не превышает нескольких процентов, а вычисление показателя корреляции рангов значительно проще, он может служить приближенной оценкой коэффициента корреляции.

При изучении корреляционной зависимости между критериями, выраженными в баллах или классовых вариантах и при большом количестве сопоставляемых пар, целесообразней r вычислять по способу сумм [141] с использованием корреляционной решетки и формулы

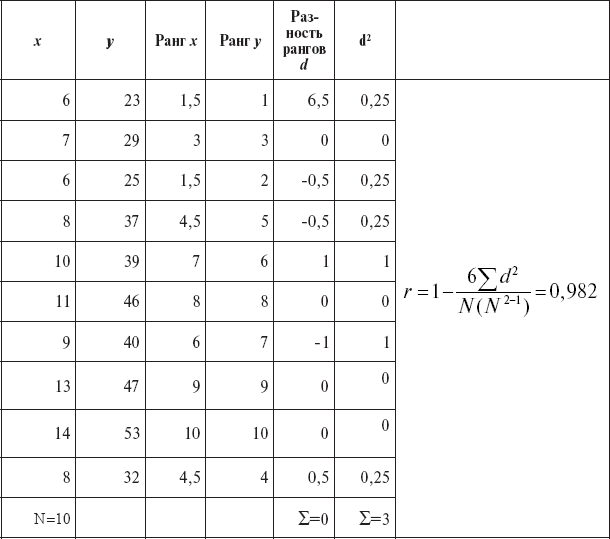
Таблица 8

Расчет показателя корреляции рангов

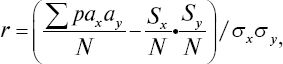
где Spa_xa_y – сумма произведений частот корреляционной решетки (P_xy) на соответствующие порядковые номера классов (баллов); S – сумма первого полного ряда накопленных частот, получаемого кумуляцией частот каждого ряда в направлении, обратном порядковой нумерации классов; ?_x и ?_y – средние квадратические отклонения рядов; N – общее число парных наблюдений.

Изучая корреляционную связь между двумя признаками x и y, необходимо помнить о возможности существования зависимости или влияния на них других варьирующих признаков. Поэтому наряду с изучением парных корреляций возникает задача измерения множественных связей между варьирующими признаками индивидуальных психофизиологических особенностей организма и критериями успешности обучения. Для решения этой задачи необходимо воспользоваться коэффициентом общей или совокупной корреляции и частными или парциальными коэффициентами корреляции.

Совокупный коэффициент корреляции между варьирующими признаками x, y и z вычисляется по следующей формуле:

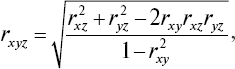
где r_xy, r_xz и r_yz – парные коэффициенты линейной корреляции между признаками x и y, x и z, y и z.

На практике чаще применяется парциальный коэффициент корреляции, измеряющий связь между двумя варьирующими признаками x и y при постоянном значении третьего – z – учитываемого признака, который может иметь или имеет связь с первыми двумя. Так, парциальный коэффициент между x и y при исключительном влиянии на эту связь, составляет

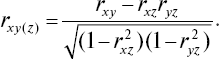
Соответственно рассчитываются коэффициенты парциальной корреляции между x и z при влиянии y– r_xz(y); y и z – при влиянии x– r_yz(x).

Как видно из приведенных формул, расчет значений совокупного и парциальных коэффициентов корреляций производится на основе парных коэффициентов корреляций.

В некоторых случаях возникает необходимость изучения связи между несколькими внешними критериями, даваемыми разными экспертами (независимые характеристики, ранжирование и др.), и ее достоверности. Например, для обеспечения объективности выведения оценки летных способностей курсантов по 9-балльной шкале по мнению четырех экспертов А, Б, В, Г из летно-инструкторского состава (командир и его заместители) необходимо определить степень совпадения их мнений в отношении одних и тех же курсантов. Для этой цели используется показатель корреляции рангов для суммарной ранжировки – коэффициент конкордации

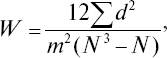
где ?d² – сумма квадратов отклонений индивидуальных сумм рангов от средней индивидуальной суммы рангов; m – число сравниваемых ранжированных рядов; N – численность выборки. W показывает степень согласия ранжированных рядов, и его значения могут колебаться от 0 до 1 (табл. 9).

В данном примере он достаточно высок (W = 0,91) и свидетельствует о единстве мнений внешних экспертов по оценке летных способностей курсантов.

В ряде случаев, когда критерии профессионально-психологической пригодности и успешности обучения не распределяются в вариационный ряд, корреляция между ними устанавливается по наличию нескольких качественных признаков в связи с качественными признаками обучения.

Корреляция между качественными признаками, группируемыми в 4-клеточную корреляционную решетку, определяется c помощью коэффициента ассоциации (r_a) Дж. Юла – тетрахорического показателя связи. Когда изучается корреляционная зависимость между несколькими качественными признаками, группируемыми в многоклеточные таблицы, используется коэффициент взаимной сопряженности (К) – полихорический показатель связи.

Таблица 9

Расчет коэффициента конкордации

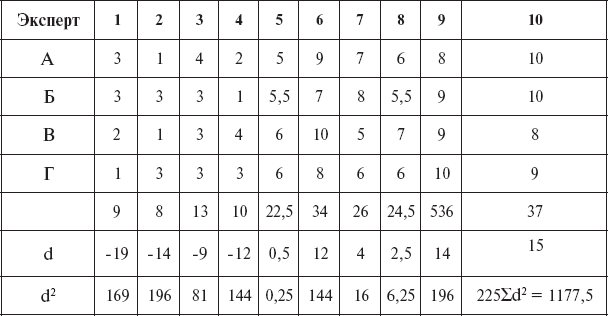
Таблица 10

Расчет коэффициента ассоциации

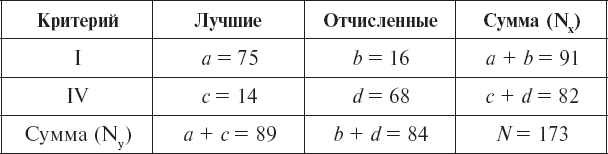
Рассмотрим пример вычисления коэффициента ассоциации при изучении связи между такими критериями пригодности, как I и IV группы, и критериями успешности обучения – лучшие и отчисленные:

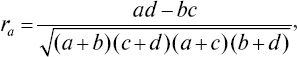
где a, b, c, d – численности альтернативных признаков (практически неограничены).

В корреляционной решетке (табл. 10) приведены исходные данные для расчетов (x – группа; y – успешность обучения).

Подставляя в формулу соответствующие значения из таблицы, находим величину коэффициента ассоциации (r_a = 0,65), который выражается в долях от 0 до 1. Достоверность оценивается по его отношению к средней ошибке, определяемой по формуле

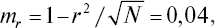
откуда t = 16,25.

Достоверность r_a может быть определена также и по специальным таблицам [52].

При изучении корреляционной зависимости между вариационными рядами с отсутствием линейной зависимости более правомерным является вычисление корреляционного отношения, которое измеряет состояние любых, в том числе и нелинейных, связей между признаками.

В отличие от коэффициента корреляции, изучающего двустороннюю связь между x и y, корреляционное отношение (?) показывает только зависимость изменений второго (y) признака от изменений первого (x), или наоборот. Корреляционное отношение – величина относительная, положительная и принимает значение от 0 до 1. Показатели корреляционного отношения обычно не равны между собой – ?_y/x ? ?_x/y. Они определяются по следующим формулам

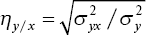
и

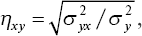
где

Эти формулы можно выразить и в другом виде:

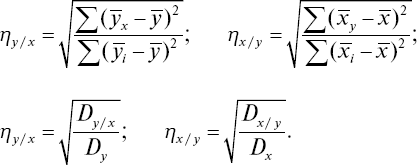
По приведенным формулам удобно определять коэффициенты корреляционного отношения для небольших выборок, а при наличии большого числа наблюдений необходимо предварительно весь материал группировать в вариационные ряды и вносить в корреляционную таблицу.

Рассмотрим вычисление корреляционного отношения на выборке из 10 наблюдений (табл. 11).

Таблица 11

Вычисление корреляционного отношения

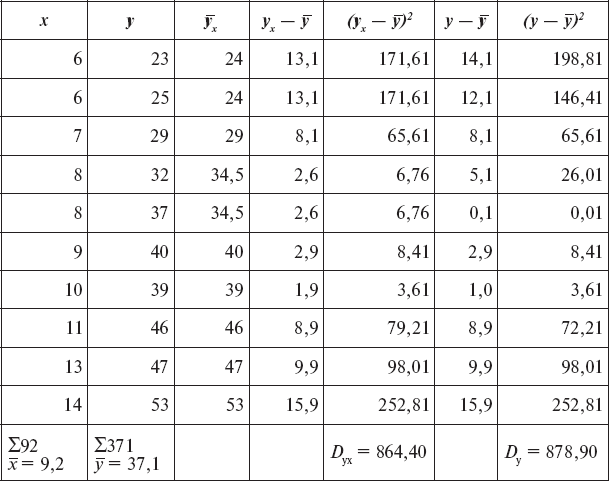
Сначала находим коэффициент корреляционного отношения полетов y по грубым ошибкам x, то есть ?_y/x, для чего ранжируем выборку по x (значения x расположены в возрастающем порядке сверху вниз). Затем определяем вспомогательные величины для вычисления корреляционного отношения по x и подставляем в формулу, откуда ?_y/x = 0,99.

Таким же способном определяем корреляционные отношения грубых ошибок x по полетам y, ранжируя выборку по y и определяем ?_y/x.

Для оценки достоверности полученных величин используем формулу

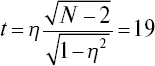
и по специальной таблице [52] находим значение P = 99,9 %.

Вычисление корреляционного отношения на больших выборках после предварительного заполнения корреляционной решетки можно производить по способу произведений, способу условных средних и способу суммирования [141].

Регрессионный анализ. Описанные показатели корреляции позволяют измерять степень связи, направление и форму существующей между ними зависимости. Однако они не дают информации о том, насколько в среднем может измениться в ту или другую сторону один из признаков при изменении другого. Такая информация представляет большой практический интерес для разработки методик психологического отбора, а также изучения влияния специальных методов подготовки на успешность профессионального обучения.

Функция, позволяющая по величине одного признака (x) находить средние (ожидаемые) значения другого признака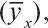 

Важную роль в регрессионном анализе играет коэффициент регрессии (R), являющийся не только параметром уравнения, но и мерой регрессии y по x и x по y. Показатели его величины (n) характеризуют зависимость между переменными x и y по их абсолютным значениям, а показатели корреляции – величины относительные и измеряют тесноту связи между признаками в долях единицы. Коэффициент регрессии характеризует только линейную связь, при которой увеличения (уменьшения) одной переменной – y– пропорциональны увеличениям другой – x, и в зависимости от направления связь либо положительна, либо отрицательна. По значениям R легко определяется коэффициент корреляции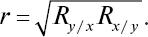 

Коэффициент регрессии позволяет рассчитать, насколько в среднем изменится признак при изменении на единицу меры другого связанного с ним признака. Он рассчитывается по коэффициентам корреляции и средним квадратическим отклонениям сопряженных видов по следующим формулам:

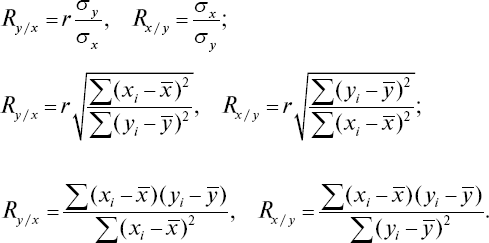
По формулам R_y/x определяется среднее (ожидаемое) значение y при изменении на единицу меры х, а по формулам R_x/y находят среднюю величину х при изменении на единицу меры признака у.

Имея возможность легко менять условия проведения эксперимента по методике у и быстро оценивать полученные результаты, мы можем установить необходимые или оптимальные условия для другой методики x – более сложной и трудоемкой. Зная интеркорреляционные связи между методиками «батареи» тестов и проводя регрессионный анализ, можно добиться оптимальных и наиболее целесообразных условий их проведения и соответственно повысить прогностичность «батареи» в целом. Например, коэффициент корреляции между результатами обследования по методике y (время – с.) и x (количество ошибок) равен +0,25; ?_y = 27, ?_x = 5. Подставляя значения в формулу, находим R_y/x = 1,35 и R_x/y = 0,995. Это означает, что увеличение времени выполнения на 1 сек соответствует увеличению количества ошибок в среднем на 0,05 ошибок, а увеличение на одну ошибку при выполнении задания соответствует увеличению времени чтения таблицы на 1,35 с.

Если сравнивать время чтения и количество ошибок по отношениям между средними арифметическими величинами этих признаков (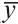

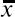
Достоверность коэффициента регрессии, как и любого другого выборочного показателя, оценивается по критерию Стьюдента с числом степеней свободы K = N–2. В обоих случаях t_y/x и t_x/y коэффициенты регрессии достоверны на 99,9 %-ном уровне.

Для прогнозирования успешности обучения и реальной деятельности (по результатам психологического обследования) может быть использован аппарат регрессионного и последовательно-дискриминантного анализа. А. Н. Лебедев разработал компьютерные программы факторного, кластерного и регрессионного анализа, которые использовались для распознавания внешнего критерия эффективности службы в системе органов внутренних дел [196].

Мерой связи между внешним критерием (например, фактором «профессионализм») и тестовым показателем служит коэффициент линейной корреляции по Пирсону. Коэффициент принимает значения от –1 до +1. Показатели связаны положительно, если с ростом одного из них возрастает и второй, и, наоборот, при росте одного и уменьшении другого. Коэффициенты корреляции рассчитываются для выборки в целом. Однако интерес представляет конкретный человек, у которого по показателям психодиагностических измерений можно было бы предсказать профессиональную успешность. Для этого используется техника регрессионного анализа.

В простейшем случае, если обозначить буквой «Д» прогнозируемую оценку профессиональной успешности конкретного человека, а «Х» – его тестовый показатель, то прогноз можно определить по формуле:

Д = r ? Х,

где r – коэффициент корреляции.

От относительных величин (нормированных) легко перейти к абсолютным. В этом случае формула регрессии принимает вид:

Д = А + кХ,

где Д и Х – нормированные показатели; А – свободный член; к – коэффициент при аргументе, то есть тестовом показателе.

Полностью поведение человека непредсказуемо, и коэффициент корреляции между внешним (рабочим) поведением и результатами отдельных тестовых измерений, как правило, составляет 0,2–0,3. Однако множество разных тестовых показателей, взятых в совокупности, связаны с прогнозируемым поведенческим качеством сильнее. Происходит совокупное усиление возможностей в задаче распознавания внешнего «образа».

Для прогноза в этом случае используется уравнение множественной регрессии типа:

Д = А + R Х₁ + m • X₂ + i • X₃ + … + q • Xn,

где Д – прогнозируемая поведенческая величина (например, уровень «профессионализма»), R, m, i, q – коэффициенты уравнения, полученные ранее на большой выборке испытуемых; X₁, X₂, X₃ … Xn – показатели тестовых измерений.

Для получения коэффициентов диагностических уравнений множественной регрессии иногда используют не всю выборку, а только полярные группы, то есть самых успешных профессионалов и тех, от которых целесообразно избавиться.

Разработанный методический подход, по мнению Б. Г. Бовина, имеет свои преимущества и недостатки [196]. Положительными качествами являются, в частности, быстрота расчета и эффективность оценивания информативности применяемых методов. Одновременно можно использовать практически любое количество показателей, из которых автоматизированная процедура позволяет сделать выбор тех, которые имеют отношение к распознаванию заданного «образа». Заданным «образом» может быть любой внешний критерий: наиболее и наименее профессионально успешные сотрудники, студенты с разным уровнем академической успеваемости, виновники аварийных ситуаций и т. п.

Другим преимуществом является достаточно полная картина статистических характеристик, получаемых на промежуточном этапе, которые позволяют исследовать многочисленные связи между используемыми параметрами. Различные психодиагностические методы могут сравниваться по тому вкладу, который они вносят в распознавание заданного «образа». В этом случае можно проверять валидность любых тестов, использование которых дает цифровой показатель.

Последнее преимущество имеет и свой недостаток – происходит определенное «выхолащивание» качественного, содержательного аспекта диагностики. Другим недостатком является нестабильность получаемых моделей распознавания. Каждая новая выборка дает новую модель распознавания неизменного внешнего критерия. В эту модель могут войти другие показатели, ранее отвергнутые в ходе регрессионной процедуры. Это создает ощущение определенной ненадежности полученных результатов. Однако эта неопределенность объясняется тем, что различные показатели обусловлены одним и тем же фактором, то есть несмотря на многовариативность моделей, содержательная сущность их сохраняется.