10.5.5. Пример

10.5.5. Пример

Проиллюстрируем на примере изложенный выше алгоритм определения профессиональной пригодности по психологическим показателям.

Разбиение на классы. В качестве исходного материала для составления дифференциально-диагностической таблицы были использованы результаты психологического обследования двух групп операторов, которых по объективным производственным показателям и характеристикам ведущих специалистов можно отнести к классу «хороших» («А») и «плохих» («В») специалистов.

Представители этих двух классов различались между собой по своей квалификации, а также, частично, по опыту работы.

Операторы, отнесенные к классу «А» (34 человека в возрасте 27–32 лет), прошли длительную подготовку по специальности и имели практический опыт работы в сложных системах управления. Все они характеризовались как специалисты высокой квалификации.

Лица, объединенные в класс «В» (33 человека в возрасте 23–29 лет), имели более низкий уровень подготовки и выполняли операторскую деятельность в менее сложных системах управления.

Психологические показатели. Для оценки состояния ряда психологических качеств и психофизиологических функций был использован комплекс табличных тестов и аппаратурных методик, выбор которых определен требованиями к состоянию ведущих систем организма у данных специалистов. Это:

1. Корректурная проба с кольцами: а) время выполнения задания в сек; б) относительная частота ошибок;

2. «Компасы»: коэффициент успешности;

3. «Отыскивание чисел с переключением»: а) время выполнения задания в сек.; б) производительность – время выполнения одной операции в сек.; в) количество ошибок;

4. «Сложение с переключением»: а) производительность – количество сложений за мин.; б) величина различия в темпе работы; в) относительная частота ошибок;

5. «Перепутанные линии»: а) производительность – количество просмотренных линий за 10 мин.; б) количество ошибок;

6. «Расстановка чисел»: а) производительность; б) относительная частота ошибок;

7. «Память на числа» – воспроизведение сразу после экспозиции: а) коэффициент успешности

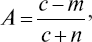
где с – общее число зафиксированных чисел, m – число ошибочно воспроизведенных чисел, n – число невоспроизведенных чисел; б) количество правильно воспроизведенных чисел;

8. «Память на числа» – воспроизведение через 30 мин. после экспозиции: а) коэффициент успешности; б) количество правильно воспроизведенных чисел;

9. «Реакция на движущийся объект»: а) относительная частота точных ответов

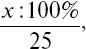
где x – количество точных ответов; б) суммарная величина отклонений от «0»;

10. Тремометрия – проведение стержня в прорези: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;

11. Тремометрия – удержание стержня в отверстии: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;

12. Рефлекс на время – 1 сек.: величина ошибки;

13. Рефлекс на время – 15 сек.: величина ошибки.

Построение распределений. Небольшое число лиц в группах «А» и «В» потребовало проведения грубого квантования, которое был сделано в соответствии с изложенными выше рекомендациями (см. 10.5.3). Диапазоны квантования приведены далее в таблице 15.

Полученные распределения, как правило, существенно отличаются от нормальных, а в ряде случаев имеют U—образную форму (например, показатель относительной частоты ошибок в корректурной пробе). Важно отметить, что для классов «А» и «В», вообще говоря, получены разные по форме распределения одного и того же признака.

Информативность признаков. Оценка признаков проводилась при помощи критерия ?².

Если P_j > 0,10, то признак считался неинформативным.

В результате анализа было установлено, что некоторые признаки мало информативны для различения классов и могут не рассматриваться. Необходимо отметить, что при других диапазонах квантования информативность признаков может быть несколько другой. Экспериментальное варьирование диапазонов в разумных пределах показало, что получающееся изменение информативности не очень существенно.

Построение диагностической таблицы. Теперь все готово для построения рабочей диагностической таблицы. Для каждого информативного признака вычисляется логарифм отношения вероятностей для значений психофизиологических признаков, попадающих в соответствующие диапазоны, то есть для j-признака и i-диапазона (градации) вычисляются по формуле

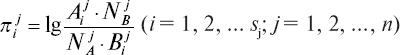
(обозначения определены выше).

Этапы последовательного вычисления диагностических коэффициентов иллюстрируются на примере одного признака (табл. 14).

Таблица 14

Пример вычисления диагностических коэффициентов

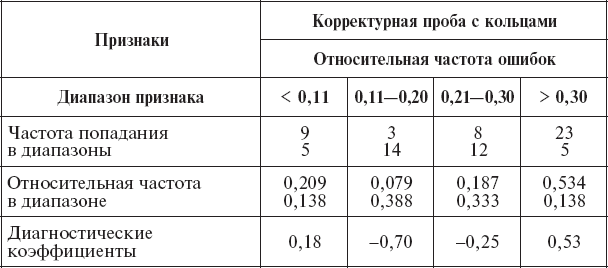
Расположение тех признаков, которые остались после отбраковки, в порядке убывающей информативности с соответствующим «диагностическим коэффициентом», сведены в таблицу 15. В ней заключается вся необходимая информация для проведения классификации на два класса «А» и «В» для новых контингентов людей.

Работа с таблицей и проверка ее эффективности. Пусть допустимые вероятности ошибок классификации a = b = 0,05. Тогда пороговыми значениями будут числа

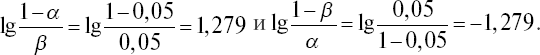
У обследуемого В-ва получены следующие психологические признаки: 1) 0,26; 2) 45; 3) 17; 4) 0,11; 5) 24; 6) 174; 7) 0,14; 8) 1,9; 9) 4,3; 10) 16 и др. (название признаков см. в таблице 15 под теми же номерами)

Находим в таблице 15 соответствующие этим значениям диагностические коэффициенты и последовательно их складываем

(-0,250) + (-0,496) + (-0,449) + (-0,604) + (-0,203)+(0,380)+ (-0,356) + (0,491)+…

Таблица 15

Значения диагностических коэффициентов (пример)

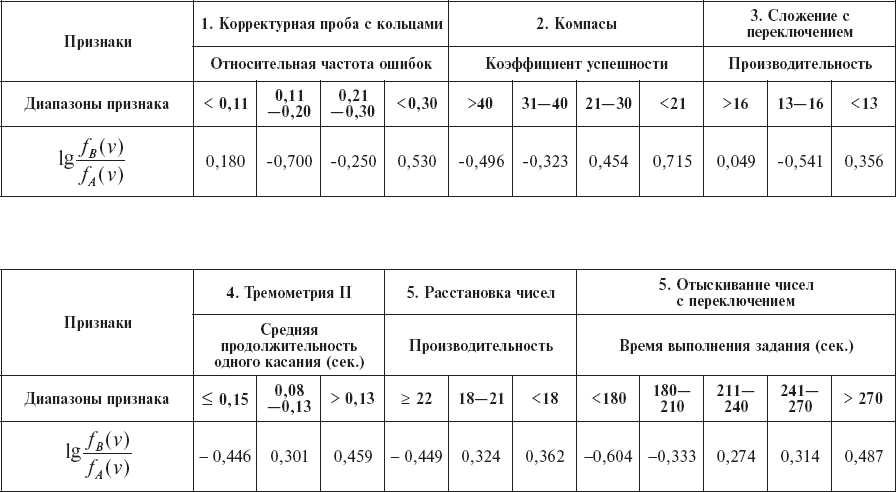
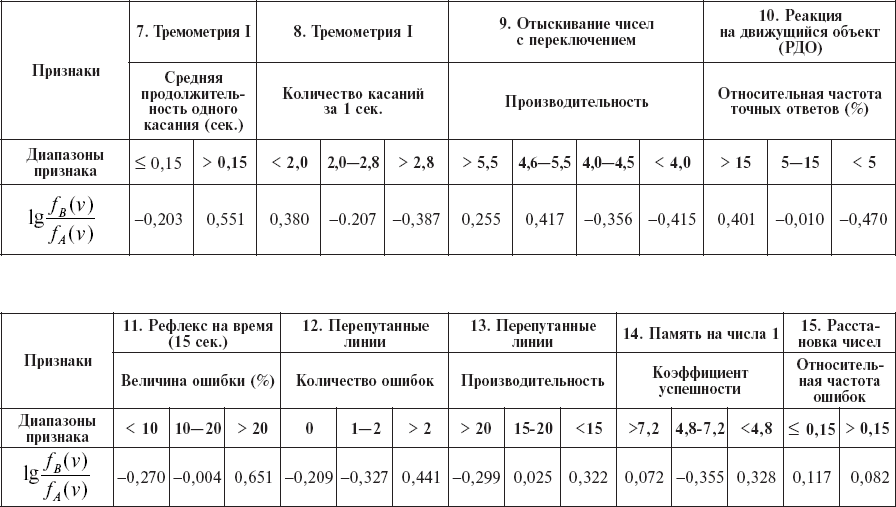
В этом примере оказывается достаточной лишь сумма первых шести признаков, чтобы превысить нижний порог с уровнем надежности P = 0,05.

Таким образом, делается вывод о пригодности обследуемого В-ва к данной операторской деятельности.

Понятно, что эта таблица может быть использована лишь для частного специального случая определения профессиональной пригодности. В других случаях необходимо построение новых подобных таблиц.

Оценку эффективности таких таблиц можно получить, проверив результаты классификации для группы лиц, данные которых послужили основой для ее составления (табл. 16).

Опыт применения классифицирующихся алгоритмов показывает, что результаты различения для проверочной группы оказываются не хуже, чем для группы обучающей [63]. Имелась возможность убедиться в этом при классификации класса «А» на основании данных повторных исследований, сделанных через 30 дней (табл. 17).

Таблица 16

Эффективность диагностической классификации (пример)

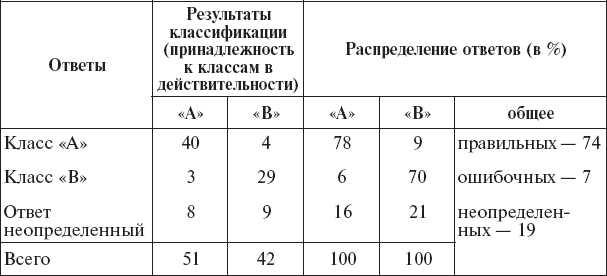
Таблица 17

Результаты повторной оценки эффективности классификации группы «А»

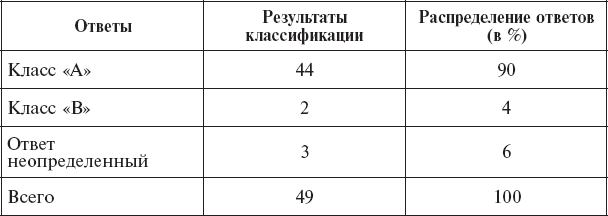
Соответствие ошибок классификации тем, которые были назначены, указывает на то, что в нашем случае статистическая зависимость между признаками мала. И действительно, вычисление интеркорреляций между признаками показало, что в подавляющем числе случаев они оказались статистически независимыми.

Имеются основания считать, что несколько худшие различения класса «В» (см. табл. 17) связаны с наличием большей зависимости между признаками в этом случае.

Таким образом, предлагаемый алгоритм можно рассматривать как реальную основу для решения конкретных задач определения профессиональной пригодности. При использовании простых вычислительных средств оказывается возможным определение наиболее прогностических методик, а после построения таблиц (подобных табл. 14), отнесение данного субъекта с заданной вероятностью ошибки к классу «А» или «В».

Пользоваться такой таблицей удобно – действие сводится к сложению трехзначных чисел. Необходимо подчеркнуть, что последовательный характер вынесения решения позволяет также последовательно получить и психологические характеристики личности, что в большинстве случаев делает излишним проведение полного набора психологических исследований. Кроме того, это также существенно экономит время проведения психологической экспертизы.

Предлагаемый алгоритм имеет определенные преимущества перед другими способами определения профессиональной пригодности не только своей вычислительной простотой и удобством, но и своей эффективностью. Дело в том, что известные математические способы, используемые для целей определения профессиональной пригодности, как правило, предполагают нормальное распределение признаков, что в действительности не имеет места. Эффективность же предлагаемого алгоритма не зависит от вида распределений, а в случае независимости признаков, по-видимому, является и оптимальным методом разделения на два класса.

Уязвимым местом многих статистических алгоритмов является их большая чувствительность к сдвигу центра распределения признаков. Такой сдвиг естественно возникает как результат различных условий проведения тестирующих исследований. Ведь совершенно ясно, что условия получения признаков в обучающих группах и в реальной ситуации могут быть весьма различны. Отношение же вероятностей мало чувствительно к однонаправленному сдвигу центра распределений, и поэтому эффективность неоднородной последовательной статистической процедуры существенно при этом изменяться не будет. Она в какой-то степени инвариантна по отношению к однонаправленному сдвигу центров:

f_А^j(v_j) и fB^j(v_j) (j = 1, 2, …, n)

В то же время необходимость обучающих групп «А» и «В» является существенным и неустранимым недостатком настоящего алгоритма и может вызвать трудности при решении некоторых задач. Другой недостаток заключается в том, что алгоритм не учитывает зависимость признаков, но этот недостаток может быть устранен при введении сложных признаков – синдромов.

Есть основания считать, что предлагаемый алгоритм будет полезным при решении и ряда других задач, возникающих в прикладной и теоретической психологии. Отметим возможность его применения для тонкой дифференциации психологических состояний на основании наблюдений большого числа признаков, каждый из которых содержит мало информации для различения.