Модельная школа
КАК ОБЪЯСНИТЬ МИР В ДВА СЧЕТА
При визуализации тех или иных моделей или явлений различают «дивергентные» и «конвергентные» рисунки.
Дивергентный, то есть «расходящийся, рисунок представляет разные возможности действий и выбора, стимулирует креативное мышление и предлагает новые решения.
Конвергентный, то есть «сходящийся», рисунок – это тот, на котором представлены только существенные принципы какой-либо теории, те или иные аспекты проблемы. Такой рисунок помогает понять самые сложные вещи, представляя своего рода их «конспект».
На следующих страницах мы продемонстрируем несколько примеров, как можно изобразить наш разнообразный мир всего несколькими штрихами.
«Цель визуализации – проникновение в суть, а не сама картинка».
Бен Шнейдерман
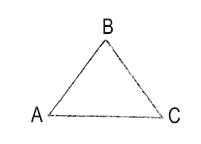
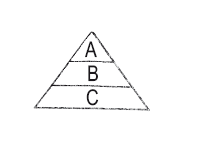
1. Треугольник
Как или почему А, В и С связаны друг с другом?
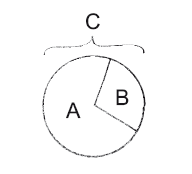
2. Секторная диаграмма
Из скольких А и В состоит С?
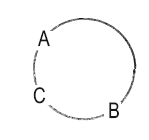
3. Круговая диаграмма
За А следует В, из В следует С, потом снова все начинается с А.
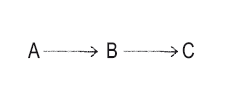
4. Причинно-следственная цепочка
С следует из В, а В из А.
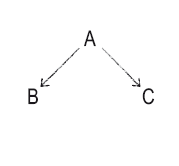
5. Блок-схема или «генеалогическое древо»
Блок-схема: если А, тогда В или С.
Генеалогическое древо: из А следует В и из А следует С.
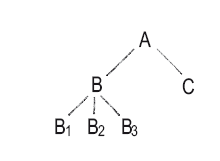
6. Диаграмма связей
Исходя из А, я вывожу В и С, из В – В1, В2, В3.
7. Концентрические круги
А – часть В, обе – часть С.
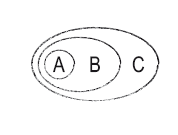
8. Диаграмма количества (диаграмма Венна)
Общность А и В, В и С, С и А и А, В и С.
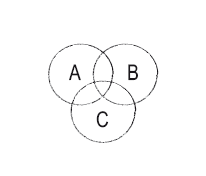
9. Динамометрический анализ
А противопоставляется В.
С поддерживает В.
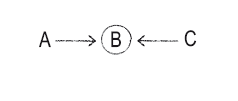
10. Линейный график
Горизонтальная ось указывает время (t), вертикальная – величину А. В и С показывают характер кривой (гауссова кривая, экспоненциальная кривая, «хоккейная клюшка» и т. п.).
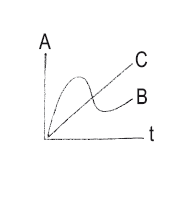
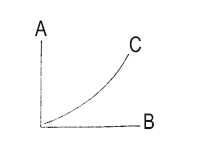
11. Двухмерная осевая модель («Cartesian coordinates»)
Оси А и В – различные параметры. Кривая С показывает их возможное соотношение.
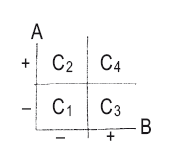
Альтернатива: матрица с четырьмя полями. При этом вместо кривых отражаются определенные позиции.
12. Трехмерная осевая модель
К осям А и В добавляется третья ось С. В систему координат могут вноситься различные показатели.
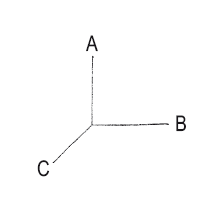
13. Полюсная модель
Параметры противоположны друг другу: черное – белое, слева – справа. Могут быть представлены различные позиции.
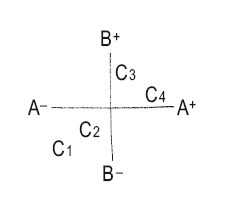
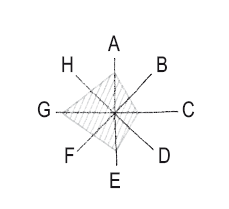
14. Диаграмма «радар», или «паук»
Показывает параметры и их соотношение. В заштрихованном виде принимает характерную форму радарного поля. Подходит для сравнений.
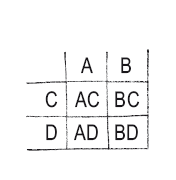
15. Таблица
Для составления списка и комбинаций А, В и С.
16. Воронка
А и В и С в итоге дают…?
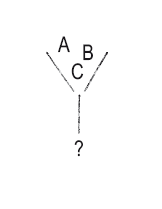
17. Мост
Как мы попадем из А в С, если есть преграда В?

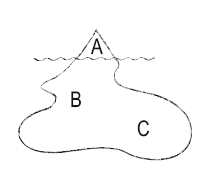
18. Айсберг
Что лежит в основании А? Что видимо? Что невидимо?
19. Пирамида
Кто дает задания С? Или: чем А узаконивает свое положение?
20. Дерево
В и С растут из А.