3.5. Анализ заданий
Анализ заданий по результатам, полученным в пилотажном исследовании, имеет своей целью отбор наилучших заданий для окончательной версии опросника и включает в себя определение доли ответивших правильно (в соответствии с ключом) и дискриминантности каждого задания. Первый шаг состоит в том, чтобы составить таблицу анализа заданий (табл. 3.3), в которой каждая колонка (а, Ь, с, d и т. д.) представляет задание, а каждая строка (1, 2, 3, 4, 5 и т. д.) – обследуемого. Когда речь идет о разработке личностных опросников, в таблицу вписывается соответствующий балл по каждому заданию, а при этом имеется в виду, что обратные задания (с противоположным содержанием) оцениваются так же, как и прямые задания, но в противоположном направлении континуума оценок. Затем суммируются баллы по каждой клетке для получения общего балла по каждому ряду (испытуемые) и общего балла по каждой колонке (задания).
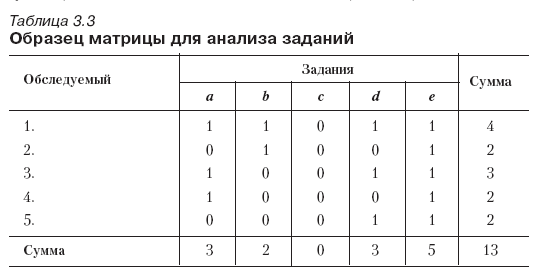
Следующим шагом будет вычисление показателя, определяющего долю испытуемых, ответивших в соответствии с «ключом» опросника или индекса эффективности задания[65]. Этот показатель подсчитывается делением количества обследуемых, давших правильный (так называемый «ключевой») ответ, на их общее количество. В идеале этот индекс для каждого задания должен располагаться в интервале от 0,25 до 0,75, приближаясь в среднем к 0,5 для всего опросника. Индекс, меньший чем 0,25, показывает, что задание неэффективно потому, что очень многие обследуемые отвечают на него правильно, а выше 0,75 указывает на то, что на данное задание получено слишком много правильных ответов. В табл. 3.3 анализа заданий индекс эффективности для каждого задания получается следующим образом: (а) 3/5 = 0,6; (b) 2/5 = 0,4; (с) 0/5 = 0; (d) 3/5 = 0,6 и (e) 5/5=1. Из этого следует, что нужно устранить задания (с) и (е) из окончательной версии опросника.
Также нужно удостовериться, просмотрев результаты в таблице анализа заданий, в том что хороший индекс эффективности, т. е. лежащий где-то посередине между крайними оценками, не просто означает выбор средних оценок в оценочном континууме каждым испытуемым, а представляет собой вариацию различных оценок.
Задания (вопросы, утверждения) только тогда следует включать в окончательную версию опросника, когда они измеряют те же самые личностные особенности, что и другие, предназначенные для этого задания. Для определения дискриминативности заданий используется коэффициент корреляции каждого задания с общим баллом всего теста. Чем выше коэффициент корреляции, тем выше дискриминантность задания, тем лучше задание. Это основной критерий. Как правило, требуется минимальная корреляция в 0,2. Задания с отрицательной или нулевой корреляцией почти всегда исключаются.
Для расчета этого показателя чаще всего применяется коэффициент произведения моментов Пирсона (заметим, что он наиболее приемлем для оценивания заданий, имеющих пять и более вариантов ответа, а в случае дихотомических заданий используется точечно-бисериальная корреляция). Вычисления обычно производятся с помощью специальных компьютерных программ, однако каждый разработчик тестов должен хотя бы один раз провести расчеты вручную. Это дает возможность проникновения в смысл того, что происходит с заданиями теста. Тем читателям, которые попытаются осуществить эту процедуру, напоминаем, что коэффициенты корреляции всегда меньше +1 и больше -1. Если получено значение коэффициента, выходящее за границы этого интервала, значит, допущена ошибка в расчетах. Формула коэффициента произведения моментов Пирсона имеет вид:
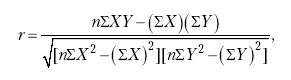
где r– коэффициент корреляции; X – результат по каждому заданию; Y– балл (результат) по всему тесту; п – количество попарных произведений; ?– сумма. Для того чтобы подсчитать коэффициент корреляции произведения моментов Пирсона, нужны: сумма баллов испытуемых по каждому заданию (?X), сумма баллов испытуемых по всему тесту (?Y), сумма квадратов баллов испытуемых по каждому заданию (?Х2), сумма квадратов баллов испытуемых по всему опроснику (?Y2), сумма произведения баллов по каждому заданию и по всем заданиям (?XY). Путем подстановки в формулу значений перечисленных показателей вычисляется коэффициент корреляции. Нижеследующий пример демонстрирует простой способ получения этого коэффициента. Для избежания ошибок рекомендуется повторный подсчет по каждому заданию.
При решении вопроса о включении задания в окончательную версию теста нужно принимать во внимание многие факторы. В дополнение к изучению эффективности и дискриминантности нужно определить то количество заданий, которое потребуется для окончательной версии (не менее 20–30 заданий!), и насколько хорошо они «вписываются» в ранее созданную для теста решетку. Например, можно включить задания с низкой дискриминативностью, если имеется немного заданий по некоторой области измерения. Также иногда имеет смысл включение в окончательный вариант опросника задания с недостаточно высоким показателем эффективности при условии, что оно обладает достаточной дискриминантностью. Также важно обеспечить приблизительно равное количество прямых и обратных заданий. Для испытуемых разных полов необходимо выполнить отдельные процедуры анализа заданий.

Способы улучшения заданий выясняются как раз на этой стадии конструирования теста. Например, изменение формулировки ответа в задании с «иногда» на «всегда» может повысить показатель эффективности. Однако эти изменения во всех вопросах (утверждениях) могут повлиять на надежность и валидность теста. Процедура анализа заданий дает необходимую информацию относительно параметров каждого задания. Тем не менее только исследователь может вынести решение о том, какой из критериев наиболее важен для реализации цели создаваемого теста.
В начале 1980-х гг., помимо традиционных процедур анализа заданий, появляются более сложные, использование которых невозможно без достаточно мощного компьютерного обеспечения. К таковым прежде всего относится теория «задание-ответ» (item response theory, IRT). Технические приемы этой теории, несмотря на продолжающиеся дискуссии, сегодня включаются во вновь создаваемые тесты. Однако речь идет прежде всего о тестировании способностей. Наиболее сложные проблемы возникают в связи с попытками приложения ITR к тестам личности. Безусловно, нельзя утверждать, что процедуры из ITR неприменимы в оценке личности, однако требуется решение многих задач, прежде чем эта теория заменит традиционные процедуры анализа заданий (подробнее об этой теории см. в работах Клайна, 1994; Анастази и Урбина, 2001; и др.).






