8.1. Популяционная генетика
Генетика популяций постулирует, что единица эволюционного процесса должна представлять собой неделимое единство и быть способной изменяться в ряду поколений. Ни вид, ни особь не удовлетворяют этим критериям. Элементарной единицей эволюционного процесса является популяция.
Популяция – это изолированная группа особей одного вида, связанная общностью территории и происхождения. Этот термин был предложен В. Иоганнсеном в 1909 г.
Представление о популяции как единице эволюции сформировалось почти сразу после возникновения дарвинизма. Популяция представляет собой непрерывный ряд поколений, она характеризуется и наследственностью, и изменчивостью. Понятие популяции применимо для организмов, как размножающихся половым путем, так и для лишенных полового процесса.
В период становления популяционной генетики считалось, что генетическая изменчивость природных популяций весьма мала, большинство локусов содержат доминантные аллели (аллели дикого типа) и лишь несколько локусов содержат мутантные аллели. Выходило, что «нормальный» генотип особи в природе гомозиготен почти по всем локусам.
В настоящее время принята так называемая балансовая теория популяций, предложенная Ф. Добжанским (Dobzhansky Тh., 1937). Согласно ей, изменчивость природных популяций очень велика, составляющие популяцию особи гетерозиготны по большинству локусов, не существует аллелей «дикого типа». При этом подчеркивается, что отсутствует какой-либо «нормальный» генотип. Генофонд популяции, включающий в себя все аллели всех населяющих популяцию особей, весьма разнообразен. Мерой генетической изменчивости популяции служит такое понятие, как гетерозиготность.
Гетерозиготность популяции показывает среднюю частоту особей, гетерозиготных по определенным локусам. Для подсчета гетерозиготности сначала определяют частоты гетерозигот по каждому локусу, а затем вычисляют среднее из полученных результатов. Чем большее количество локусов будет исследовано, тем более точная оценка изменчивости популяции будет получена. Исследования показали, что для приблизительной оценки достаточно проанализировать около 20 локусов.
Гетерозиготность – надежный показатель изменчивости. Она определяет вероятность того, что два любых аллеля одного локуса из генофонда популяции, взятые наугад, будут разными. Средняя гетерозиготность популяций человека составляет 6,7 % (Айала Ф., Кайгер Дж., 1988).
Таким образом, популяция – это совокупность генотипов, различающихся по многим локусам. Большинство локусов характеризуются множественными аллелями. Такое явление получило название полиморфизма. Количественным выражением полиморфизма популяции служит полиморфность (Р), показывающая долю полиморфных локусов. Так, если в исследованной популяции из 40 локусов 8 локусов оказались полиморфными (представленными несколькими аллелями), а 32 – мономорфными (представленными одним аллелем), то Р = 0,2, или 20 %.
Полиморфизм не выражает в полной мере степень генетической изменчивости популяции. Все локусы, имеющие больше одного аллеля, при вычислении Р будут равнозначными. Однако один локус может иметь в популяции 2 аллеля, а другой – 20. Не изменяет Р и относительная частота аллелей при одинаковом их числе. Аллели могут быть более-менее равномерно представлены в популяции, а может наблюдаться явное превалирование одного аллеля над всеми остальными.
Как и в случае многих других генетических терминов, различие между понятиями «мутация» и «полиморфизм» достаточно условное. Обычно, если какая-нибудь последовательность ДНК встречается чаще, чем в 1 % случаев, то говорят о полиморфизме, если реже, чем в 1 %, то о мутации. В геноме человека среднее число вариаций для каждого гена равняется 14 (Тарантул В. З., 2003). Значительным полиморфизмом характеризуется и число различных повторов, что у человека играет важную диагностическую роль.
Важнейшей характеристикой популяции являются показатели частот аллелей и генотипов составляющих ее особей. Их позволяет рассчитать ключевой закон популяционной генетики – закон Харди – Вайнберга. Он гласит, что при случайном скрещивании и отсутствии внешних факторов частота аллелей в популяции постоянна.
Для обозначения частот аллелей в популяционной генетике используются специальные символы: р – частота аллеля А; q – частота аллеля а; тогда p + q = 1.
Зная частоты аллелей, можно рассчитать частоты генотипов. Вероятность получения каждого генотипа равна вероятности объединения соответствующих гамет.
Для расчета частот генотипов применяют формулу квадрата двучлена:
(p + q)2 = p2 + 2pq + q2,
где p2 – частота генотипа АА; 2pq – частота генотипа Аа; q2 – частота генотипа аа.
Применение закона Харди – Вайнберга для расчета частот аллелей у человека наглядно демонстрирует пример аутосомно-рецессивных болезней. Зная частоту встречаемости генетического заболевания, по формуле Харди – Вайнберга мы можем рассчитать частоту аллелей (с поправкой на погрешность). Например, одно из тяжелейших аутосомно-рецессивных заболеваний человека – муковисцидоз, встречается с частотой 1: 2500. Поскольку все случаи проявления обусловлены гомозиготой рецессивного аллеля, то:
q2 = 0,0004; q = 0,02;
p = 1 – q = 1–0,02 = 0,98.
Частота гетерозигот (2pq) = 2 ? 0,98 ? 0,02 = 0,039 (около 4 %).
Мы видим, что почти 4 % людей (совсем не мало) являются носителями гена муковисцидоза. Это показывает, сколь большое число рецессивных патогенных генов находится в скрытом состоянии.
При множественном аллелизме частоты генотипов определяются возведением в квадрат многочлена из частот аллелей. Например, имеются три аллеля: а1, а2, а3.
Их частоты соответственно: p, q, r. Тогда p + q + r = 1.
Для расчета частот генотипов:
(p + q + r)2 = p2 + q2 + r2 + 2pq + 2pr + 2rq,
где p2 – частота генотипа а1 а1; q2 – частота генотипа а2 а2; r2 – частота генотипа а3 а3; 2pq – частота генотипа а1 а2; 2pr – частота генотипа а1 а3; 2rq – частота генотипа а2 а3.
Необходимо отметить, что сумма частот генотипов, как сумма частот аллелей всегда будет равна 1, т. е. (p + q)2 = (p + q + r)2 = =… = 1. Частоты генотипов остаются неизменными в последующих поколениях.
Если число аллелей одного локуса обозначить k, то число возможных генотипов (N) можно рассчитать по специальной формуле:
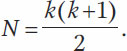
В строгом виде закон Харди – Вайнберга применим только для идеальной популяции, т. е. достаточно большой популяции, в которой осуществляется свободное скрещивание и не действуют внешние факторы. Только при этих условиях популяция находится в равновесии. Такие идеальные условия в природе никогда не реализуются. Рассмотрим подробнее два ограничения применения закона Харди – Вайнберга, касающиеся свободного скрещивания и действия внешних факторов.
В генетике популяций выделяют два вида скрещиваний:
1. Панмиксия – свободное скрещивание: вероятность образования брачной парыне зависит от генотипа партнеров. В отношении целых генотипов панмиксия в природе почти никогда не соблюдается, однако она вполне применима в отношении отдельных локусов.
2. Ассортативность – избирательное скрещивание: генотип влияет на выбор брачного партнера, т. е. особи с определенными генотипами спариваются чаще, чем при случайной вероятности. Избирательное скрещивание не изменяет частот генов, но изменяет частоты генотипов. Одной из крайних разновидностей ассортативности является целенаправленный инбридинг – скрещивание между родственными особями. Применительно к человеку ассортативность будет рассматриваться в разделе психогенетики.
Отклонение от равенства Харди – Вайнберга свидетельствует о том, что на популяцию действует какой-либо внешний фактор. Для анализа изменений генных частот в настоящее время разработаны сложные и довольно громоздкие системы уравнений. Это объясняется наличием переменных факторов, влияющих на результат. Разновидности эволюционных факторов мы рассмотрим чуть ниже, а пока отметим, что в любой достаточно большой популяции отклонения будут весьма незначительны, поэтому закон Харди – Вайнберга позволяет проводить важнейшие расчеты и является основой популяционной генетики. Но эти отклонения становятся значимыми, когда мы начинаем рассматривать процесс в эволюционном масштабе времени. Динамика генофонда популяций и представляет эволюцию на генетическом уровне.






