5
Сортировка почты

Чарли Магна не успевает закончить свои почтовые дела. Сейчас уже середина дня, июль, Кейптаун. Температура 45 °C. К тому же рассеянный и неуклюжий Чарли выронил коробку с отсортированными письмами и перемешал пачки, которые нужно доставить 33 адресатам в его округе. Но и это не все: у почтальона повышенная чувствительность к солнечному свету, а он забыл кепку и солнцезащитные очки дома. Стоя на коленях на раскаленной гальке, он собирает конверты и пытается разложить их в нужном порядке, чтобы закончить работу, прежде чем на коже появятся волдыри.
Подсказка: подумайте, как можно разбить одну большую проблему на несколько маленьких.
Порядок поможет нам управиться с задачей быстрее. Представьте, что было бы, если бы местная газета не анонсировала предстоящие события по дням недели. Если бы серии телесериала, которые вы планируете посмотреть, не перечислялись в телепрограмме. Как было бы досадно тратить время на поиски следующего эпизода, вместо того чтобы посмотреть очередную историю о неудавшемся наркодилере, получившем еще один удар от жестокой вселенной.
Давайте посмотрим, как Чарли может справиться со своей неожиданной поблемой.
ЦЕЛЬ: СНОВА РАЗЛОЖИТЬ РАССЫПАННЫЕ ПАЧКИ КОНВЕРТОВ В НУЖНОМ ПОРЯДКЕ
МЕТОД 1: ПОЛОЖИТЬ ОДНУ ПАЧКУ НА ЗЕМЛЮ ПЕРЕД СОБОЙ. ВЗЯТЬ ВТОРУЮ ПАЧКУ, И, ЕСЛИ МЕСТО ЖИТЕЛЬСТВА АДРЕСАТА БЛИЗКО К ПЕРВОМУ, ПОМЕСТИТЬ ЕЕ СЛЕВА. И ТАК ДАЛЕЕ, ПОКА САМЫЕ БЛИЗКИЕ АДРЕСА НЕ ОКАЖУТСЯ СЛЕВА ОТ ЛИНИИ, А САМЫЕ ДАЛЕКИЕ – СПРАВА.
МЕТОД 2: РАЗЛОЖИТЕ ПАЧКИ КОНВЕРТОВ В РЯД ПЕРЕД СОБОЙ. РАЗДЕЛИТЕ ИХ ТАК, ЧТОБЫ СПРАВА И СЛЕВА ОКАЗАЛОСЬ ОДИНАКОВОЕ КОЛИЧЕСТВО КОНВЕРТОВ. ЗАТЕМ РАЗДЕЛИТЕ КАЖДУЮ ГРУППУ ПОПОЛАМ. КЛАДИТЕ БЛИЗКИЙ АДРЕС СЛЕВА, А ДАЛЕКИЙ – СПРАВА. ЗАТЕМ ДЕЛАЙТЕ ЭТО ДЛЯ КАЖДОЙ ПАРЫ ПАР И ТАК ДАЛЕЕ.
Вот как эти два метода выглядят на графике:
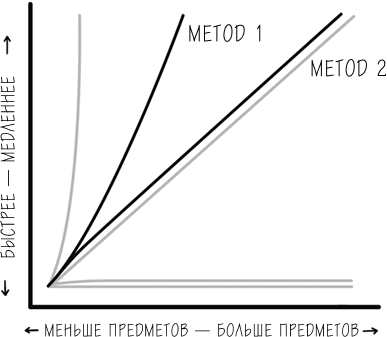
В реальной жизни при сортировке каких-либо вещей вручную, как это делает Чарли, допустимы некоторые вариации метода 1, которые он скорее всего использовал бы. Как мы видели из прежних сравнительных графиков, общее правило таково: для сортировки нескольких вещей годится любой метод. И только когда предметов много, один из методов может оказаться намного лучше другого. Хотя метод 2 не всегда имеет практическую корреляцию в реальной жизни, по крайней мере при сортировке, мы обсудим общий подход в концептуальных терминах.[23]
Для начала заметим, что метод 1 несет в себе определенный ритм. Чарли берет одну пачку конвертов, затем просматривает другие пачки, чтобы определить, куда ее положить. Затем он берет другую пачку конвертов, просматривает остальные пачки и так далее. Мы видели подобный подход раньше, когда разбирали носки, не так ли? Разница в том, что с каждым конвертом Чарли просматривает все другие только один раз, в то время как с носками Марджи могла потратить много времени, выискивая к каждому пару в куче белья.
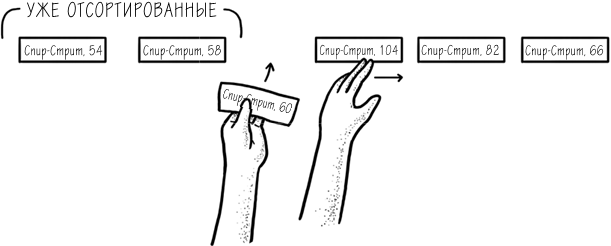
Подход Чарли в методе 1 – характерная черта алгоритма с квадратичным временем.[24] Каждый раз, когда у вас есть набор предметов (независимо от того, одинаковые ли они или разные) и вы перебираете их все в поисках одного, у вас есть алгоритм с квадратичным временем. Другие примеры подобного алгоритма – примерка нескольких рубашек с целью выбрать подходящую к вашим брюкам или сравнение списка покупок с продуктами на полке в магазине.
В информационных технологиях многие простые способы сортировки данных протекают в квадратичном времени. Подобно методу 1 Чарли, они все работают путем сравнивания смежных пунктов и перемещения их в зависимости от того, какой больше, а какой меньше. Все подходы, построенные на принципе сравнения прилегающих точек, в среднем происходят в квадратичном времени (n2). Иначе говоря, если n – количество конвертов, мы можем описать функцию, которая располагает эти конверты в нужном порядке с помощью сравнения, как «ограниченные n2», то есть в среднем (это ключевое слово!) мы не можем это сделать быстрее. Существует также сортировка методом вставок, методом выделения и пузырьковым методом.
Когда я впервые услышал о сортировке, будучи 16-летним школьником, я сперва не понял, что может быть лучше метода с квадратичным временем. График показывает, что метод 2 значительно быстрее, чем метод 1, поэтому стоит сортировать элементы в субквадратичном времени.
Общий подход к субквадратичному способу сортировки подразумевает такие методы, как разделение и присваивание, то есть разбивание группы предметов на более мелкие группы и сортировку этих групп.[25] Разделение группы пополам есть логарифмический метод, как мы видели ранее, а помещение предметов в одну группу снова – линейный, так как мы берем один предмет один раз. Этот подход к сортировке называют линейно-логарифмическим, и можно представить, что он гораздо быстрее, чем метод с квадратичным временем и немного медленнее, чем метод с линейным временем.[26] Его можно называть лог-линейным, или просто n log n, – этот порядок складывается из времени, затрачиваемого на разделение группы (log n) и на компоновку предметов заново (n). При умножении они дают n log n. Слово «линейно-логарифмический» образовано из двух: «линейный» и «логарифмический». Это создает концепцию, более сложную, чем составляющие ее части, – совсем как с Джедвардом.[27]
Два хорошо известных линейно-логарифмических алгоритма – сортировка слиянием, изобретенная Джоном фон Нейманом в 1945 году, и быстрая сортировка, придуманная Тони Хоаром в 1959 году. Метод 2 для Чарли сходен с сортировкой слиянием. Этап разделения соответствует раскладыванию пачек конвертов на отдельные кучки. А этап обратного слияния – сравнению и совмещению этих пачек. На последнем этапе в первый раз у нас остается набор двух упорядоченных групп. Во второй раз мы получаем уже четыре упорядоченные группы. В случае с Чарли процесс будет выглядеть так:
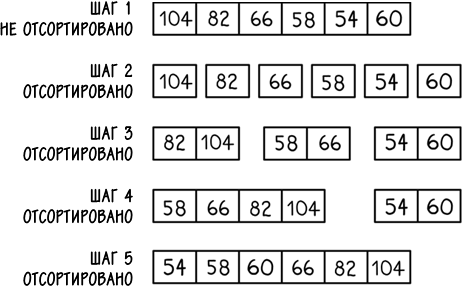
Заметьте, как он переходит от набора неотсортированных конвертов в первом этапе к набору отсортированных конвертов, хоть и одного размера, на втором. На каждом последующем этапе он совмещает группы, создавая все более длинные ряды отсортированных конвертов, пока у него не останется один ряд, содержащий все конверты. Если мы рассмотрим поближе один из таких этапов, например этап 4, то сможем увидеть, как происходит слияние.
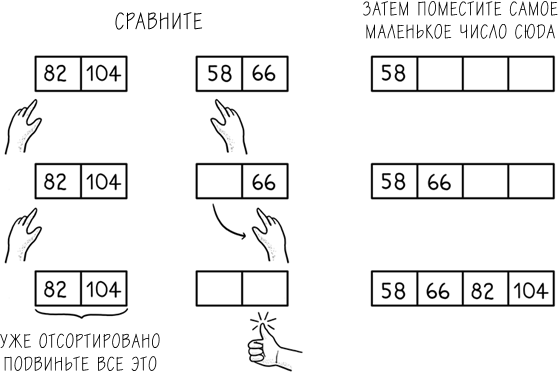
И все же метод 2 – лучший выбор исходя из увеличения скорости, которого он позволяет достичь. Преимущество Чарли в том, что у него всего 33 пачки конвертов для сортировки. Любой метод спасет его от недельных страданий из-за обожженной кожи. Если бы у него было больше конвертов, то скоростной метод 2 оказался бы более предпочтителен, и Чарли, несомненно, извлек бы пользу от знания, как быстрее сортировать почту. Ну, а пока он заканчивает свой рабочий день.

ЗАВЕРШАЯ РАЗВОЗКУ ПОЧТЫ, ЧАРЛИ СЧАСТЛИВ КАК НИКОГДА: СЕГОДНЯ ОН УЗНАЛ КОЕ-ЧТО НОВОЕ. «ВЕЗДЕ ЕСТЬ МЕСТО ДЛЯ ОТКРЫТИЙ, – ГОВОРИТ ОН СЕБЕ, – ДАЖЕ ТАМ, ГДЕ НЕ ОЖИДАЕШЬ».

ПОЛЬЗУЙТЕСЬ НА ЗДОРОВЬЕ. ТОНИ ХОАР. ИЗОБРЕТАТЕЛЬ МЕТОДА БЫСТРОЙ СОРТИРОВКИ






