7
Обнови статус

Некто Дуэйн отправился в поход по Скалистым горам Канады. Здесь кристально чистые озера с бирюзовой водой прячутся в лесной чаще, а в воде отражается все величие грандиозных гор и деревьев. Птицы щебечут, порхая в чистом небе, а с запада дует нежный бриз. В такие моменты кажется, что весь наш мир – царство тишины и покоя. Как будто нигде не льются реки крови, нет всемирного потепления и нищеты. «Идеалисты правы, – шепчет проплывающая в небе тучка, – несомненно, правы».
И все же мысли Дуэйна витают далеко отсюда. Сегодня утром, когда группа выдвинулась из Ванкувера, ему довелось стать свидетелем необычного зрелища. Он видел, как утка прохаживалась вдоль берега, виляя хвостом, как будто танцевала румбу. С тех пор нет ему покоя – он изо всех сил старается составить смешное, но в то же время короткое предложение, чтобы описать всю прелесть сцены, используя не более 140 символов. Такое ограничение диктует прибор, созданный для того, чтобы расширить нашу свободу. Дуэйн не может подвести армию незнакомцев, на чье восхищение он рассчитывает.
Мозг, как утверждают нейрологи, обладает способностью выделять во всем отличительные черты. Когда в тихой комнате вы слышите какой-то шум, ваш мозг фиксируется на нем. Если вы находитесь в шумной комнате и слышите звук, непохожий на другие шумы, то ваше сознание непременно вычленит его. Информация, которая встречается часто, обычно рассматривается мозгом как менее значимая, и он отфильтровывает ее поток.
Метод, которого придерживаются многие, печатая эсэмэски с пропуском часто встречающихся букв, например гласных, частично основан на положении из теории информации. Оно гласит, что «длжна передвться тлько инфрмция сущствнная для ншго понмния». Благодаря избыточности языка предыдущее предложение понятно, потому что пропущенные буквы можно угадать. Поэтому, когда нам надо сократить текст и не потерять суть, как в случае с Дуэйном, такой подход вовсе не так уж плох. Именно так мы делали до появления системы упрощенного набора текста.[30] Но вместе с экономией места этот подход приводит к потере данных, пусть неинформативных и несущественных.
До сих пор мы говорили о более быстрых или более медленных способах выполнения задач, а сейчас речь пойдет о вещах, которые занимают больше или меньше места. Этот баланс важен для оценки различных подходов к решению проблем: часто ученые-компьютерщики сравнивают скорость разных методов (временна?я сложность выполнения задачи), но иногда оценивают, как много памяти или места на диске эти методы занимают (пространственная сложность).
ЦЕЛЬ: СОЧИНИТЬ ОСТРОУМНУЮ ФРАЗУ-СТАТУС, КОТОРАЯ СОДЕРЖИТ НЕ БОЛЬШЕ 140 СИМВОЛОВ.
МЕТОД 1: ЗАМЕНЯТЬ ДЛИННЫЕ СЛОВА НА КОРОТКИЕ, НО МЕНЕЕ ТОЧНЫЕ.
МЕТОД 2: ОПУСКАТЬ ЧАСТО ВСТРЕЧАЮЩИЕСЯ БУКВЫ, НАПРИМЕР ГЛАСНЫЕ, В НЕКОТОРЫХ СЛОВАХ.
Поразительно, но у метода 2 есть аналог в информационных технологиях. В 1952 году ученый Дэвид А. Хаффман изобрел способ сокращения пространства, необходимого для хранения данных. В отличие от прежних методов алгоритм Хаффмана не требовал удаления информации, а концентрировался на оптимизации.
Компьютеры хранят словесную информацию, кодируя буквы алфавита, цифры и другие символы и занося их в таблицу, где им присваиваются числовые значения. Эти значения затем сохраняются в том виде, какой понимает компьютер, – он называется бинарным, или двоичным, кодом. Каждый символ в нем представлен в виде кода, который может состоять из семи бит. Например, буква «а» английского алфавита имеет значение 97, а в двоичном коде запись этого числа выглядит так:
1100001
Буква «b» имеет значение 98 и в двоичном коде она такая:
1100010
Если бы нам нужно было представить слово «hans» в двоичном коде, то оно бы выглядело так (каждая буква занимает 7 бит, всего 28 бит):
1101000 1100001 1101110 1110011
То обстоятельство, что символы имеют двойные коды одинаковой длины (в нашем случае 7 бит), позволяет легко декодировать бинарную цепочку. Все, что нам нужно сделать, – считывать каждые семь бит и затем, используя таблицу соответствий, перекодировать их в слова английского языка.
Но Хаффман был хитер. Он посмотрел на эти семь бит и сказал: «Конечно, должен быть способ сжимать данные». Друзья отговаривали его. «Нет, Хаффман, – говорили они. – Этого нельзя сделать. Ты слишком многого хочешь. Не рвись в герои». Но Хаффман не слушал их. Он был готов броситься с головой в неизвестность, чтобы изобрести другое бинарное представление набора символов.

Вместо использования бинарных кодов с фиксированной длиной Хаффман стал применять бинарные коды разной длины. Он опирался на факт, что некоторые символы встречаются в письменной речи чаще, чем другие, поэтому он присвоил этим часто встречающимся буквам меньшие величины. Соответственно они имели более короткий бинарный код, а реже встречающиеся символы – более длинный.
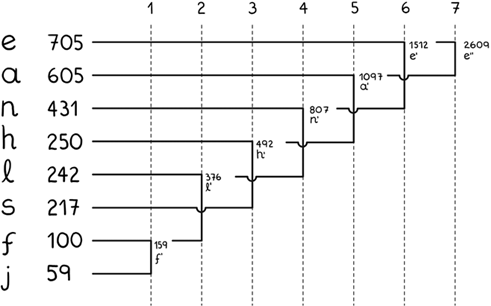
Например, для нашего набора данных частота встречаемости символов распределяется так, как показано на таблице слева.
Буква «е» встречается нам 705 раз, буква «а» – 605 раз и так далее. Заметьте, что символы отсортированы сверху вниз в порядке убывания частоты. Согласно подходу Хаффмана, нужно взять пару символов с наименьшей частотой встречаемости, сложить их значения, сохраняя результат в новом вре?менном символе, а затем отсортировать набор. Процесс повторяется, пока у нас больше не останется пар символов.
В конечном итоге получается дерево, где каждый узел (символ) соединен с парой узлов, на основе которых он образовался, с двумя краями. Если мы произведем такую операцию с приведенным выше набором данных, то в конечном итоге получим что-то вроде схемы, где мы сначала соединяли «f» и «j», затем результат этого действия совмещали с «l» и так далее. Каждая колонка, начиная со второй, представляет собой один шаг алгоритма.
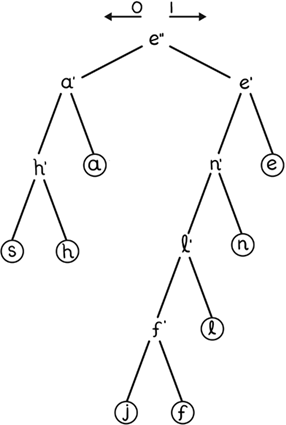
Когда мы преобразуем схему в дерево, все становится яснее. Оптимизированный двоичный код символа – это цепочка, которую мы получаем, считывая биты с самого верхнего, или корневого,[31] узла и двигаясь ниже к узлу символа. Каждый раз, когда мы двигаем дерево влево, мы прибавляем ноль к двоичному коду символа, а при движении вправо добавляем единицу. Поэтому буква «е» заканчивается двухбитным двоичным кодом 11, а буква «f» представляет собой пятибитный код 10001. Приписывание 1 или 0 к дочернему узлу дерева Хаффмана производится факультативно, то есть литера «е» может быть закодирована как «01», а не как 11. Несмотря на то что двоичные коды не всегда уникальны, они считаются наиболее оптимальными. В любом случае дерево Хаффмана отсылается адресату вместе с сообщением, чтобы получатель знал, как его раскодировать.
Вот список оптимизированных двоичных кодов. Заметьте, что самые частые буквы имеют наиболее короткие коды.

Как же будет выглядеть слово «hans» в двоичном коде?
001 01 101 000
Для такой записи нам понадобилось 11 бит, а не 28. Это открытие заставляет вспомнить историю почти столетней давности о том, как передавали сообщения по телеграфу. Способ Самюэля Морзе кодировать буквы также был основан на том, насколько часто эти буквы встречались в английском языке. Морзе определял частоту различных букв не в ходе бесед с учеными или анализа данных – он просто считал литеры в шрифтовой каретке наборщика в типографии. Так что в следующий раз, когда какой-нибудь умник начнет критиковать ваши методы исследования, не отступайте.
Техники компрессии данных, подобные кодированию методом Хаффмана, чрезвычайно важны в современном мире. Оптимальное использование пространства означает, что вебсайты будут загружаться быстрее, веб-серверы могут сжимать файлы, прежде чем рассылать их по сети, а современные браузеры сумеют легко распаковывать их. Если место ограниченно, любое увеличение скорости имеет значение.
Компрессия также означает, что фильмы (то есть файлы формата MPEG-2), изображения (файлы формата JPEG) и песни (файлы формата МРЗ) могут занимать меньше пространства, что позволит сэкономить деньги на их хранении и пересылке. Аудиофайлы типа МРЗ интересны в том плане, что их сжатие основано на удалении того диапазона аудиосигналов, который человеческое ухо не может услышать из-за особенностей своего анатомического строения. Например, оно не воспринимает частоту свыше 20 000 Гц.
В следующий раз, когда вы будете разговаривать по голосовой или видеосвязи с высоким качеством звука и изображения, подумайте о том, что ваша беседа стала возможной благодаря конверсии. Технология достигла такого уровня, что вашему приложению нужно всего лишь послать данные по сети, а потом либо догадаться о содержании, либо реконструировать оставшуюся часть на другом конце. На самом деле компрессия помогает снизить барьер использования технологий.
Все это хорошо. Но что там с Дуэйном и его читателями? Останутся ли они довольны? К счастью, да. Парень удачно выкрутился из ситуации и успешно описал сцену – событие, его юмор и важное сообщение, предназначенное для тех, кто хотел его услышать. Сила написанного слова – вот за что был сожжен на костре Уильям Тиндейл.[32] Парень обновляет свой статус, и сотни нетерпеливых пользователей получают долгожданный хит.
«В фантастическом походе с самого рассвета. Лучшее: утки устроили бесплатное шоу».
Остается надеяться, что умение Дуэйна сжимать сообщения без потери важной информации всегда будет приводить к такому же успешному результату. Если нет, уткам придется его научить.







