10
Возьми коробку

Людвик продает компьютерные товары в магазине на Миссион-Стрит. Он живет рядом на 14-м этаже сорокаэтажного жилого комплекса, где все помещения общего пользования находятся под видеонаблюдением. Чтобы зарабатывать и покрывать расходы на растущую аренду, Людвик часто подбирает картонные коробки из склада утильсырья в своем доме и использует их для отправки модулей памяти клиентам за границу. Помещение для утиля есть на каждом этаже здания.
Недавно поступил заказ, который нужно выполнить сегодня, а почта закрывается через 15 минут. Людвику нужно срочно найти картонную коробку для посылки.
ЦЕЛЬ: ПРОЙТИ КАК МОЖНО МЕНЬШЕ ЭТАЖЕЙ, ЧТОБЫ НАЙТИ ПУСТУЮ КОРОБКУ.
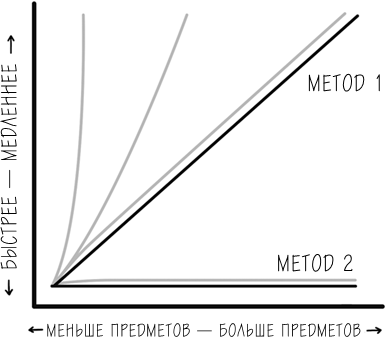
МЕТОД 1: ПЕРЕХОДИТЬ С ЭТАЖА НА ЭТАЖ В ПОИСКАХ КОРОБКИ.
МЕТОД 2: ПОПРОСИТЬ ВАХТЕРА ПОСМОТРЕТЬ ЗАПИСИ КАМЕР ИЗ ПОМЕЩЕНИЙ УТИЛЬСЫРЬЯ.
Давайте обсудим, как Людвику достичь цели и найти коробку в своем здании.
Метод 1 – это внутренний алгоритм Людвика. Он начинает с верхнего этажа и идет вниз, преодолевая по одному лестничному пролету. Время, которое потребуется для выполнения задания по этому методу, можно разделить пополам, если попросить друга просмотреть четные этажи, а сам Людвик в это время займется нечетными. Но такой алгоритм остается линейно-временным по причинам, которые мы рассмотрим немного позже.
Метод 2 предлагает более удачный алгоритм и позволяет Людвику выяснить, в какой из комнат есть пустые коробки, если он попросит вахтера просмотреть записи камер. Такой алгоритм дает возможность найти пустую коробку в постоянное время, а не в линейное, так как для этого придется посетить только один этаж. Звонок на вахту – постоянная единовременная цена, которую заплатит Людвик, чтобы избежать линейного роста времени.
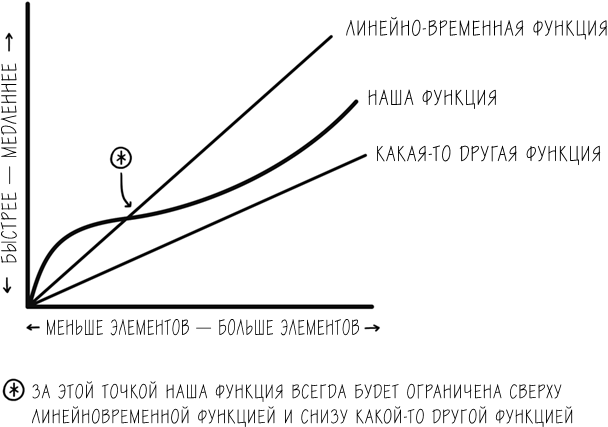
Возможно, настал момент обсудить способ, с помощью которого мы измеряем скорость роста. В этой книге мы намеренно идем на упрощение ради ясности. Но все равно важно понимать, что есть разные пути для описания скорости роста определенного алгоритма или функции. Один из них известен как «нотация большой теты» (Big-Theta Notation) и характеризует функцию посредством установки верхнего и нижнего предела. Для большого числа элементов он означает, что функция может расти не быстрее, чем линейная функция (n) или логарифмическая функция (log n), и не медленней, чем другие функции,[39] с которыми она связана.
Поэтому мы позволяем себе утверждать: «Бинарный поиск лучше линейного, потому что в худшем случае он занимает логарифмическое время». Как мы видели в главе 2, бинарный поиск (метод логарифмического времени) позволяет нам найти рубашку на вешалке с сотней рубашек за семь шагов, а на гипотетической вешалке с тысячью рубашками – всего за десять шагов или около того. Сравните это с сотней и тысячью шагов соответственно в случае линейного поиска.
Есть два момента, которые предполагает нотация большой теты. Первое: она опускает коэффициенты, объясняя, что их значения становятся непоследовательными по мере увеличения количества предметов.[40] Итак, степень роста n или n/2 будет характеризоваться линейным временем и записываться как ?(n) – читается «большая тета n». Второе: большая тета рассматривает только главный член в функции, предполагая, что он максимально воздействует на результат функции по отношению к другим членам. До сих пор мы называли этот главный член основной операцией. Приводя пример из информатики, профессор Марк Вайсе разъясняет этот вопрос:
В функции 10N3+N2+40N+80, для N =1 000 величина функции есть 10 001 040 080, из которых 10 000 000 000 приходится на член 10N3.
Итак, если метод 1 заставляет Людвика посетить этаж, где он живет, скажем, два раза, мы охарактеризуем время, которое уходит у него на достижение цели в худшем случае как t(n)=n+1, где +1 обозначает этот дополнительный визит, и он записывается в нотации большой теты как ?(n).
Это допущение требует нескольких оговорок.
Например, бывают случаи, в которых второстепенные члены оказывают серьезное влияние на функцию. Вспомните Джо и ее ожерелье из главы 9. Мы сконцентрировались на добавлении бусин и рассматривали первый метод как линейно-временной, а второй – как постоянно-временной и при этом более привлекательный. Мы по умолчанию признавали, что склеивание свободных концов шпагата было простым заданием – но если клею нужно пять минут, чтобы схватиться? Повлияет ли это на выбор Джо? Такие постоянные величины наиболее заметны, когда мы имеем дело с малым числом элементов и должны учитывать их наличие.
Две другие нотации, которые дополняют большую тету и оперируют при тех же условиях, – большая омега и большая о. Большая омега устанавливает нижнюю границу функции для достаточно большого значения n, то есть она говорит, что наша функция может расти не медленней, чем ее нижняя граница. Большая о определяет верхнюю границу функции для достаточно большого значения n, то есть говорит о том, что наша функция может расти не быстрее, чем верхняя граница. Конечно, в действительности функция может расти медленней, чем верхний предел и, таким образом, быть более привлекательной, но большое о – пессимист и воплощение закона Сода.[41]
Когда мы говорим о скорости роста алгоритма, мы имеем в виду его действенность в худшем случае, когда он тесно связан, по оценке большой теты. Заметьте, что любой уровень скрытности, двуличия, обмана, который мы допускаем в этой книге, порождает компромисс. Важно знать, что в реальности больше нюансов, чем в теории, – об этом можно прочитать в источниках, перечисленных в конце книги. Что касается Людвика, то различия в двух алгоритмах очевидны, что делает решение его проблемы достаточно легким.