4
Выход из лабиринта

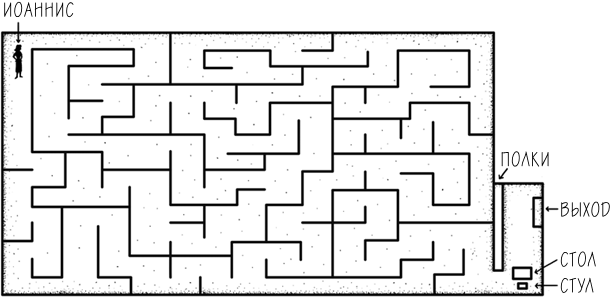
Как-то раз один портной, грек по имени Иоаннис, заблудился в собственной мастерской. Мастерская пользовалась большой популярностью среди афинян, а сам Иоаннис имел репутацию скряги и скопидома. Ситуация осложнялась тем, что помещение располагалось на обширном участке земли, постепенно занимая его, по мере того как Иоаннис в течение 30 лет строил новые проходы и ставил стеллажи для удовлетворения своей страсти к накопительству. И вот он попался: сидит в созданном им же самим лабиринте, заваленном хламом, а вокруг выстроились полки с бесконечными рядами ниток, одежды и разломанных швейных машин. Как же Иоаннису найти путь обратно? Или ему суждено погибнуть здесь?
Есть еще одна греческая история. Когда родился Минотавр, полубык-получеловек, великий архитектор Дедал построил лабиринт, куда было заточено это злое и коварное существо.
«Оказавшись внутри, он бродил по извилистым тропинкам, но так никогда и не нашел выхода. В это место периодически отправлялись молодые афиняне, которых отдавали на съедение Минотавру. И не было у них никакой возможности спастись».
К счастью для Тесея, который тоже должен был стать жертвой Минотавра, дочь царя Ариадна влюбилась в него и разработала план его побега.
Она послала за Дедалом и велела ему показать выход из лабиринта. Тесею она обещала спасение, если он возьмет ее в Афины и там женится на ней. Ариадна дала ему ключ, полученный от Дедала, и клубок пряжи, который Тесей должен был прикрепить к двери и разматывать нить по мере продвижения. Так он и сделал и, конечно же, когда понадобилось, смог проделать путь в обратном направлении. Он смело прошел по лабиринту, нашел Минотавра спящим, убил его и вышел наружу».
Запомните эту историю. Мы скоро вернемся к ней снова. А пока давайте опишем три метода, которые Иоаннис мог бы использовать, чтобы найти выход из мастерской.
ЦЕЛЬ: ВЕРНУТЬСЯ К ВЫХОДУ
МЕТОД 1: ИДТИ ПО ПРОХОДАМ. СВОРАЧИВАТЬ НАУГАД, ПОКА НЕ НАЙДЕШЬ ВЫХОД.
МЕТОД 2: ДЕРЖАСЬ ПРАВОЙ РУКОЙ ЗА СТЕНУ, ИДТИ ВДОЛЬ НЕЕ, СВОРАЧИВАЯ КАЖДЫЙ РАЗ ТОЛЬКО НАПРАВО.
МЕТОД 3: ВЗЯТЬ С ПОЛКИ КАТУШКУ С НИТКАМИ И РАЗМАТЫВАТЬ ЕЕ ПО МЕРЕ ДВИЖЕНИЯ ПО ПРОХОДУ. ЕСЛИ ПОПАДЕШЬ В ТУПИК ИЛИ НАТКНЕШЬСЯ НА СВОЮ ЖЕ НИТКУ, ТО ПОВЕРНУТЬ НАЗАД И ПОЙТИ ПО ДРУГОМУ ПРОХОДУ.
Метод 1 имитирует путь мыши в лабиринте. Никаких продвинутых умственных способностей для него не требуется – просто беспорядочное хождение от одной точки до другой, пока по случайности не наткнешься на кусок сыра. Иногда его так и называют – метод беспорядочной мыши. Как вы можете догадаться, результат достигается крайне медленно.
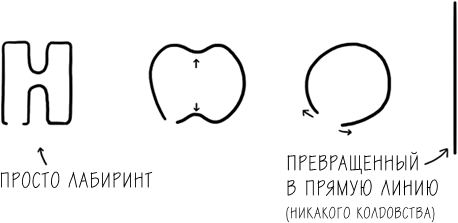
Метод 2 немного интереснее, хотя тоже довольно прост. Здесь Иоаннис идет по стене, держась за нее рукой, и находит дорогу к выходу. Почему это срабатывает? Потому что, если развернуть стены лабиринта, получится прямая линия, и, шагая вдоль нее, когда-нибудь достигнешь конца.[18]
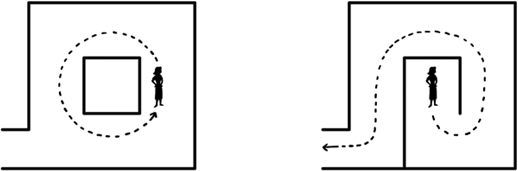
Хоть метод 2 и быстрее метода 1, его проблема в том, что в лабиринте могут быть так называемые островки или петли – внутренние стены, которые не соединены с внешними. В 1820 году граф Стэнхоуп построил в Чевенинге (Кент) первый садовый лабиринт с такими петлями. Его целью было создать лабиринт, из которого нельзя выйти по методу 2.
Таким образом, в некоторых лабиринтах этот метод, известный как стенохождение или правило правой руки,[19] может подвести человека и не привести к желаемому результату.
Краткое отступление. Интересно, что Чарльз Дарвин почти двадцать лет изучал все возможные контраргументы к своей теории эволюции, прежде чем опубликовал «Происхождение видов». Исследование такого масштаба сродни хождению по лабиринту, где развилки тропинок соответствуют предположениям,[20] где тупики означают, что аргумент не выдерживает критики, а выход – понимание, что вывод верен. Оказалось, что этот когнитивный подход к аргументам и контраргументам также работает, если применять его для поиска выхода из реального лабиринта. И это в точности то, что мы видим в методе 3 и в истории о нити Ариадны.
При помощи этого метода Иоаннес ведет обратный учет, который помогает ему тянуть нить: когда он попадает в тупик, он может вернуться и пойти по другому пути.[21] Возможность вернуться к месту пересечения ходов и попробовать более удачный путь гарантирует, что Иоаннес рано или поздно найдет дорогу обратно. Эта стратегия нахождения выхода из лабиринта называется алгоритм Тремо, ей мы обязаны французскому математику Эдуарду Лукасу и его книге «Математические рекреации», изданной в 1882 году.
Недавние исследования доказывают, что другие существа (например, муравьи) тоже могут использовать что-то типа метода обратного отслеживания для нахождения пути, если тропинка обрывается. Этот способ быстрее метода 1 и помогает выбраться из замкнутых петель в отличие от метода 2.
Заметьте, что эти три метода полезны, только когда главная цель – выбраться из лабиринта. Есть и другие способы поисков выхода, которые могут быть гораздо быстрее, однако при их применении требуется знать, как устроен лабиринт. Кроме того, методы, которые мы рассмотрели, не гарантируют нахождения самого короткого пути из лабиринта.
В мире есть десятки настоящих лабиринтов, некоторые простираются на многие мили, и там усвоенные нами уроки можно применить на практике. Но вышеперечисленные методы могут пригодиться и в других ситуациях. В более общем виде идея прохода от одной точки до другой в замкнутом пространстве, похожем на лабиринт, выглядит так. Это сеть или график как альтернативный способ описания лабиринта, где проходы – края, а пересечения – вершины, находятся в ядре многих приложений, которыми мы пользуемся и полагаемся на них каждый день. Приложение, которое знает, как соединены дороги – OpenStreetMap, например, – может подсказать кратчайший путь от вашего дома до пляжа. Веб-сайт, который знает, как связаны люди, места и вещи – скажем, Google’s Knowledge Grap, – дает лучшие результаты поиска: интернет-сайт, который знает, кто ваши друзья – Facebook или LinkedIn, например, – может догадаться, с кем еще вы знакомы, а программа, которая знает, как соединены ее компоненты и модули – скажем, Firefox, – предвидит, где вероятнее всего проявятся дефекты в будущем, основываясь на паттернах и плотности соединений.
Даже роботы-пылесосы служат хорошим примером. Не все они одинаковы. Уровень сложности зависит от того, как много пространства они способны охватить. Самые простые пылесосы бродят беспорядочными линиями или кругами, в то время как более продвинутые сначала составляют карту комнаты, определяя, где находятся стены, углы и повороты, а потом ездят взад-вперед по принципу решетки. Иными словами, когда робот знает, как лучше всего добраться с одного конца комнаты в другой, это приближает его цель, а результат – более чистая комната.[22]
В случае с Иоаннисом он выберется из лабиринта и не сойдет с ума, независимо от того, каким методом воспользуется. Но если он продолжит бесконтрольно копить хлам, а его лавка будет и дальше разрастаться, то ему придется все время ходить по ней с клубком ниток в кармане.








