Я положу свой массив в твой массив, чтоб ты не стартовал, не спросив
До сих пор мы говорили о массивах как о фундаментальной структуре, предназначенной для хранения набора элементов. В главе 6 мы ввели еще одну полезную структуру под названием матрица, которая также нужна для хранения групп элементов. Но здесь они сохраняются в двух измерениях, а не в одном. Что общего у этих двух структур? А то, что массив может быть преобразован в матрицу. Все, что нужно для этого сделать, – вместо сохранения литер (как, например, цифра, буква или слово) в каждом расположении сохранить массив. Массив массивов называется двумерным, или в более общем виде многомерным массивом.
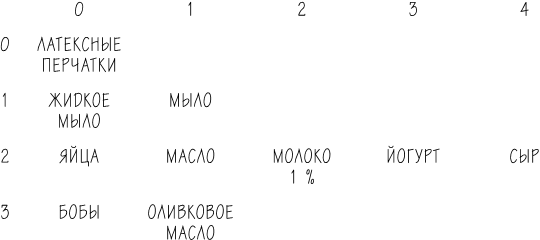
Многомерные массивы позволяют нам с Вурзмой сделать одну полезную вещь – сохранить список покупок в двух измерениях, что позволит нашему герою двигаться по любому подмассиву в зависимости от отдела, в котором он сейчас находится.
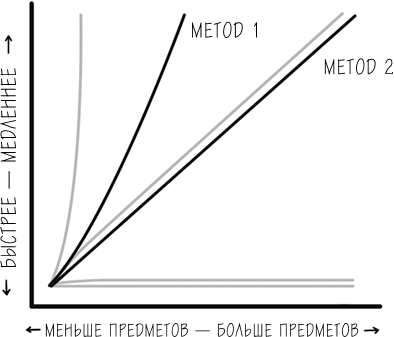
Итак, список покупок из простого перечня пунктов становится списком категорий, причем каждая из них, в свою очередь, представляет собой список пунктов.[43] Поскольку продукты в магазине обычно группируются по категориям, Вурзма может просто отправиться в ту часть магазина, где находятся, например, предметы личной гигиены, пробежаться по массиву под названием «личная гигиена» и взять нужные ему вещи со стеллажа. То же самое – для всех остальных покупок. Вот как занимаются шопингом по методу 2. Если бы Вурзма использовал обычный список – массив, как в методе 1, то он бы бродил примерно 13 минут от одного ряда к другому, в худшем случае – просто изучая полки.
Вурзма проходит мимо всех стеллажей для покупки одного предмета из списка. Если n – число проходов, а m – количество пунктов в списке, тогда n/2 ? m=(nxm/2). Иными словами, для покупки 20 вещей Вурзма проходит через 20 рядов 20 раз. Принимая во внимание, что для прохождения каждого ряда требуется 2 секунды, то потерянное время составит до 13 минут. С методом 2 его общее время на ходьбу между рядами составляет примерно минуту, так как он не появляется в одном и том же ряду больше одного раза. Вурзма в лучшем случае проходит все ряды один раз, то есть n/2. Так что для приобретения 20 наименований покупок Вурзма, идя от одного ряда к другому, теряет меньше минуты.
Заметьте, что метод 1 не выглядит в точности как сортировка по квадратичному времени, которую мы видели в главах 5 и 11. Он следует шаблону, заставляя Вурзму в худшем случае пройти по всем рядам в магазине для каждой покупки в его списке. Вот как сравниваются два метода: