11
Заполни полки
Терри учится на втором курсе престижного вуза Medlock High в Беверли-Хиллз (Калифорния). Он наказан (оставлен после занятий) за затеянную на лекции по социологии провокационную дискуссию на тему «Не во всем должны быть авокадо и капуста». В качестве воспитательной меры куратор отправил Терри в школьную библиотеку и велел выставить книги на только что купленную полку. Старая полка недавно обрушилась, и около 250 книг оказалось на полу. Все, что нужно сделать второкурснику-бунтарю, – выстроить книги на полке в алфавитном порядке по фамилиям авторов. Терри собирается вечером сходить в кино с друзьями и не хочет застрять в университете до полуночи. Ему удастся все сделать, но нельзя терять ни минуты.
ЦЕЛЬ: ВЫСТАВИТЬ ВСЕ КНИГИ НА ПОЛКУ В АЛФАВИТНОМ ПОРЯДКЕ.
МЕТОД 1: ВЗЯТЬ КНИГУ И ПОСТАВИТЬ ЕЕ НА ПОЛКУ. ВЗЯТЬ ДРУГУЮ И ПОСТАВИТЬ ЕЕ ПЕРЕД ИЛИ ПОСЛЕ ПЕРВОЙ, В ЗАВИСИМОСТИ ОТ ФАМИЛИИ АВТОРА. И ТАК ДАЛЕЕ.
МЕТОД 2: ИСПОЛЬЗОВАТЬ КНИЖНЫЕ ДЕРЖАТЕЛИ, ЧТОБЫ ОСТАВЛЯТЬ МЕСТО ПОСЛЕ КАЖДОЙ БУКВЫ АЛФАВИТА, ЗАТЕМ СТАВИТЬ КНИГИ, ПЕРЕМЕЩАЯ ДЕРЖАТЕЛИ ПО МЕРЕ НАДОБНОСТИ.
Давайте вначале решим, как Терри может поступить с заданием. Мы видели в главе 15, что подходы к сортировке, которые строятся на сравнении смежных элементов и определении, какой из них больше, а какой меньше, занимают квадратичное время. Мы говорили, что примеры такого подхода на практике включают в себя сортировку вставкой, сортировку выбором и пузырьковую сортировку и что все они работают, используя образец с минимальными различиями. Метод 1 Терри – это тот же подход, что и метод 1 Чарли из главы 5.
Здесь интересно, что усовершенствованный метод Терри не останавливается на алгоритме разбивания, как в случае с Чарли. Он модифицирует оригинальный алгоритм квадратичного времени. Это происходит при внедрении относительно простой инновации. Если мы возьмем такой алгоритм, как сортировка вставкой, мы обнаружим, что самым медленным действием будет помещение элемента на правильное место. Каждый раз после того, как мы делаем это, приходится менять расположение всех последующих элементов, передвигая их один за другим.
Что происходит при применении метода 2 Терри? Он заранее учитывает эти сдвиги, создавая пустые пространства по всей длине полки через равные промежутки. Найдя нужное место для вставляемой книги, Терри, вероятнее всего, передвинет лишь несколько других книг. Чем больше и шире эти свободные пространства, тем меньше книг ему придется сдвигать каждый раз.
Эта модернизация метода сортировки путем вставки ведет от алгоритма квадратичного времени к линейно-логарифмическому «с высокой вероятностью», как выразился его автор, и называется библиотечной сортировкой. Вспомните идею из главы 10: расставление книжных держателей по полке может сделать этот подход медленнее, если книг мало, но при их достаточно большом количестве он обладает преимуществом перед альтернативным алгоритмом.
Вот как два этих подхода выглядят на графике:
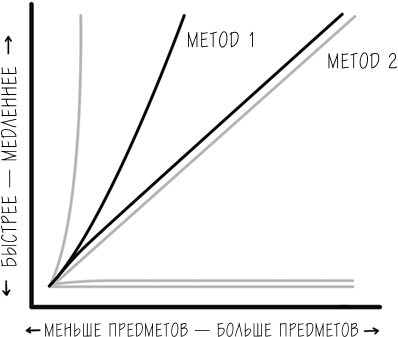
Возможно, мы лучше поймем выигрышность этого подхода, рассмотрев альтернативный, чуть более ограниченный сценарий. Вот какую мрачную картину рисуют авторы библиотечной сортировки: технологическая индустрия накрылась медным тазом, мир устал от ее глупых идей. Тысячи уволенных работников нашли убежище в некоем месте, где применяют свои таланты в обмен на бесплатную пиццу с приправами. Приток специалистов привел в восторг университеты по всей стране. Все рады, кроме архивариуса в том самом колледже. Да, пятнадцать лет назад его звали Терри. Он заведует полками с ячейками, которые промаркированы именами всех выпускников кафедры, расположенными в алфавитном порядке, и затем двигает поверх всех остальных лейблов один.
Теперь, когда частота движения ячеек достигла космической скорости, Терри вспомнил об алгоритме, который он применял когда-то в школе. Он признает, что подобный подход поможет снизить его стресс за счет высвобождения свободного пространства. И вот он создает пустые кармашки между занятыми ячейками.[42]
Недавнее упоминание о «высокой вероятности» подводит нас к важной теме и одновременно сути этой главы. Прежде мы мимоходом упоминали о «худших случаях» и «средних случаях» для разных алгоритмов. Эти существенные показатели позволяют спрогнозировать, сколько времени уйдет у определенного алгоритма на перебор всего ряда элементов.
Время осуществления алгоритма зависит от многих условий. Например, в коде мы можем столкнуться с присутствием логических ветвей (если это не ваш случай, то пропустите этот абзац). Исходя из того, какой путь выбран, время пробега может варьироваться. Хороший пример – быстрая сортировка, которая упомянута в главе 5. При быстрой сортировке разделение начинается в первую очередь с выбора опорного элемента. Этот элемент используется для разделения массива данных на две группы: в одной содержатся элементы меньше опорного, в другой – больше него. Когда опорный элемент выбирается наугад, быстрая сортировка в среднем случае проходит в логарифмическом времени. Если опорный элемент слишком велик или слишком мал, быстрая сортировка может идти в квадратичном времени в худшем случае. Это изменение в производительности происходит из-за того, что опорный элемент не справляется с разделением массива элементов на каждом этапе, и приходится проверять почти каждый элемент на каждом из тех этапов, которые, как мы видели в ранних главах, являются атрибутами квадратичного алгоритма.
Анализ быстрой сортировки показывает, что алгоритм имеет высокую вероятность прохождения в линейно-логарифмическом времени. Мы знаем, что нужно сделать, чтобы достичь этого, – убедиться, что опорный элемент не является самым верхним или самым нижним в массиве. Таким образом элемент с усредненным значением применим практически для всех случаев и может гарантировать, что быстрая сортировка пройдет в линейно-логарифмическом времени.
Но иногда вероятной гарантии все же недостаточно. Если наш алгоритм работает с таким приложением, как управление космическим шаттлом, или представляет угрозу для чьей-то жизни, регулирует работу инфузионного насоса или дефибриллятора, то показатель наихудшего случая будет нас сильно беспокоить. Классификация потенциального результата полезна и в других приложениях, применимых в повседневной жизни.
Для Терри средний случай линейно-логарифмического времени более чем предпочтителен, хотя поиск по его алгоритму в худшем случае будет проходить в квадратичном времени. Сейчас ему не о чем волноваться. Пока у него достаточно книжных разделителей, он успевает в кино вовремя.







