Думаешь, куда пойти потом? не волнуйся, я тебе покажу направление, так что поторопись
Нужно подчеркнуть еще одну вещь: многомерный массив заранее навязывает нашим элементам приоритет, а именно – расстояние от входа магазина до конкретного ряда, где находится нужная вам вещь. Возможно, пора расширить наши знания об очередях с приоритетом, о которых мы упоминали мимоходом в главе 8. Там мы говорили, что, когда вы составляете некий приоритизированный список элементов, а после нужно добавить к нему новый элемент, может понадобиться стереть некоторые части списка, чтобы освободить место. Довольно скоро дело заходит в тупик, и вы обнаруживаете, что нужно делать новый список. Как может машина составить такой список с эффективностью, которую мы ждем от нее?
Мы уже видели структуры, оптимизированные для быстрого просмотра (массивы) и вставки элементов в произвольных точках (связные списки). Теперь подробнее рассмотрим очередь с приоритетом, которая оптимизирована для добавления элемента высшего приоритета[44] к коллекции в логарифмическое время. Она называется очередью, даже если не является таковой в привычном представлении, то есть когда первый предмет, вставший в очередь, первым же из нее выходит.[45] Вместо этого вы можете представить очередь с приоритетом как некое подземное растение, которое пускает только один побег за один раз и позволяет проходящим мимо людям сорвать его.
Когда мы принимаемся за задание высшего приоритета, дерево перестраивается и выталкивает наверх задание второй приоритетности, и так далее. Этот способ описания очереди с приоритетом называется пирамидой. Мы не можем объяснить принцип пирамиды при помощи аналогии, но это замечательная структура. Нам стоит оценить, как она умеет перестроиться и вытолкнуть наверх элемент первоочередной приоритетности в логарифмическом времени, обеспечивая возникновение вставок также в логарифмическом времени.
Давайте смоделируем приоритизированный список в виде пирамиды.
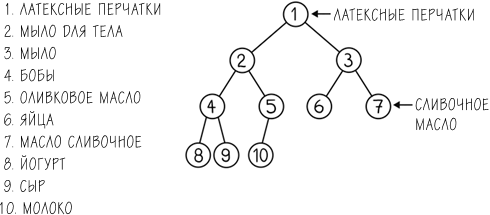
Заметьте, что пирамида представляет собой как бы дерево из узлов. У них есть две особенности. Первое: каждый узел имеет более низкий приоритет, чем родительский.[46] Поэтому пункт с самым большим приоритетом, то есть продукт, расположенный ближе всего ко входу в магазин, помещен на самом верху. Ничего больше не сообщается о порядке других узлов, таких как узлы, которые находятся на одном уровне. Есть другие структуры, они гарантируют, что все узлы в древоподобной структуре упорядочиваются, как бинарное дерево поиска, полезное в ситуациях, которые мы описывали в главе 2.
Второе свойство: каждый узел имеет два дочерних, с возможным исключением самых низших узлов. Этот структурный инвариант гарантирует, что высота пирамиды, то есть самый длинный возможный путь, не будет превышать log n, где n есть номер элементов в пирамиде.
Вот что происходит, когда Вурзма берет коробку перчаток – вещь, которая, как мы определили, лежит ближе всего ко входу, – и хочет узнать, что из списка взять следующим.
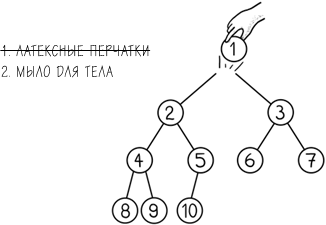
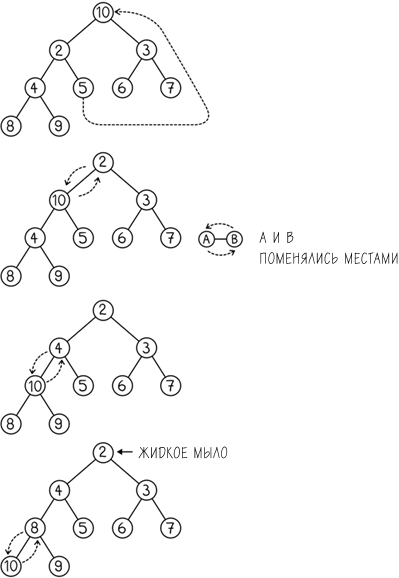
Как только мы удалили наивысший узел, первое свойство пирамиды уничтожается и активируется алгоритм повторной перестройки, который подразумевает замену пустого корневого узла последним узлом в пирамиде. Далее следует проверка нового корневого узла и его сравнение с дочерними, чтобы понять, нужно ли их поменять. Эта проверка и замена производятся с каждой парой, состоящей из родительского узла и самого малого из двух дочерних узлов все время, по мере продвижения к последнему узлу в пирамиде. Заметьте, что этот процесс перестройки пирамиды занимает логарифмическое время[47] и приводит к тому, что следующая самая близкая вещь оказывается наверху.
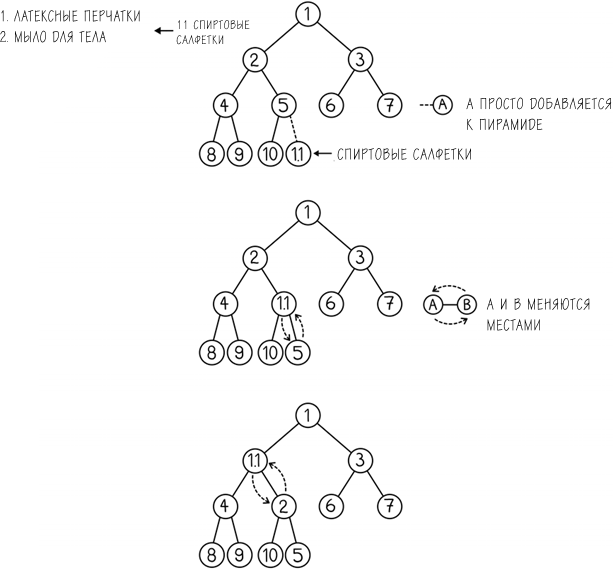
То же самое происходит, если нам нужно вставить новый приоритетный пункт в список, не стирая и не передвигая другие без необходимости, за log n число движений. Мы добавляем новый пункт в конец пирамиды и затем меняем местами с его родительским узлом, если он вдруг оказывается больше, чем новый пункт. Мы продолжаем менять их при необходимости до самого корневого узла.
В этой книге мы говорили об элегантных подходах, которые может использовать компьютер при решении какой-либо задачи. Нужно снова вспомнить о них, чтобы подчеркнуть: алгоритмы могут иметь все свойства, присущие искусству, – красоту, изящество и грацию. Если вы достигнете более продвинутых областей, где алгоритмы играют большую роль, обращайте внимание не только на результаты и производительность, но и на способы их составления. В мире искусственного интеллекта приложения алгоритмов включают в себя постановку более быстрых диагнозов в больнице, спасение жизни пациентов или исследования, дающие представление о геноме человека. В мире теории игр приложения работают на компании кратковременной аренды автомобилей, где принимают решения, как объединить пассажиров, которым нужно одновременно ехать одинаковым маршрутом. Мир компьютерного будущего занимается проектировкой беспилотных автомобилей или изобретает новые способы обработки изображений, выходящие за рамки простых трансформаций яркости и контраста. Приложениям нет границ в прикладном использовании.
Что же касается Вурзмы, то его карьера рэпера скоро начнется. Никто прежде не думал о сочинении рэпа как о массивах, хеш-таблицах и очередях с приоритетом. А ведь это может быть круто! Вурзме предстоит рассказать об этом своему сыну, которого он хочет поразить своим выступлением на рэп-баттле, в тот день, когда мальчику исполнится 11, то есть на следующей неделе. Да, что-то может пойти наперекосяк. Но самое главное: Вурзма стал быстрее управляться с покупками и делает все так хорошо, что его готовящийся к выпуску сингл пронизан самомнением. Вот и молодец.
Больше никаких игр, никаких шуток, я новый человек,
Феникс, возрожденный из пепла,
Давай начистоту, как Билл Хикс,[48]
Я так быстр, что трудно поверить, от варенья до салфеток «Клинекс»,
Хлеб, молоко и мед, органический сахар и печенье-ассорти,
Вижу: все глядят на меня, в удивлении и шоке,
Но твой стыд слишком велик, чтобы ты смог признать это,
И это норм,
Ты лишь критик себя самого,
А я – киношка Майкла Бея.[49]






