Секретный код красоты: число ? (фи)
Возможно, вы видели ряд Фибоначчи в фильме «Код Да Винчи», где героиня-криптограф находит последовательность чисел, которую ее дедушка написал на полу невидимыми чернилами на месте гибели: 1, 1, 2, 3, 5, 8, 13, 21. Последовательность строится путем сложения двух предыдущих членов и растет бесконечно. Если бы несчастный прожил еще немного, то, наверное, успел бы написать еще и 34 — сумму 13 и 21. Ищете универсальный код пропорционального роста? Эта последовательность чисел — ваш святой Грааль.

При бесконечном продолжении последовательности отношение двух последних членов сходится к иррациональному числу, приблизительно равному 1,618033988. Это золотое сечение, которым греки и египтяне пользовались, проектируя идеально сбалансированные произведения строительного искусства, приводящие в изумление даже современных архитекторов. Золотое сечение обозначается греческой буквой ? (фи).
Египтяне и греки поклонялись числу ? как истоку вечной красоты и называли его божественной пропорцией. Парфенон и другие великие архитектурные произведения древности, сохранившиеся до наших дней, отчасти сохранились именно потому, что их строили, соблюдая математический принцип идеальной пропорции; архитекторы и по сей день изучают их с восхищением. Философ Сократ считал геометрию, в которой число ? играет важнейшую роль во взаимоотношении разных форм, не только руководящей константой природного мира, но и потенциальным источником самой жизни. Леонардо Да Винчи был одержим геометрическими отношениями и структурой человеческого тела; его знаменитый эскиз «Витрувианского человека» — мужское тело, наложенное на круг и квадрат, — показывает, что он тоже искал «природный код», создающий живые формы.
В поисках идеального лица доктор Марквардт обнаружил, что золотое сечение уникально еще и тем, что создает симметрию особого типа — динамическую симметрию. Согласно теории восприятия, существует два способа создать гармонический баланс в предмете или пространстве. Первый способ — разделить его на равные части, создав симметрию равновесия. Пример такой симметрии — двухлучевая симметрия (см. иллюстрации на стр. 76). Второй способ — разделить его согласно золотому сечению, создав идеальную форму асимметрии — идеальную потому, что отношение меньшей части к большей точно такое же, как большей части к целому (см. иллюстрацию ниже). Это динамическая система. Что интересно, динамическая симметрия характерна для роста живой материи, а симметрия равновесия — для роста кристаллов.
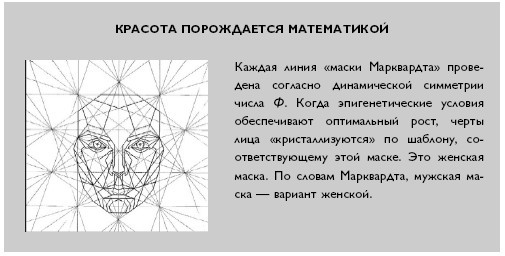
В литературе о человеческой красоте часто говорится о двухлучевой симметрии: если одна сторона является идеальным отражением другой, значит, у вас красивое лицо. Но это ошибка, и вот почему: динамическая симметрия, конечно, часто приводит к двухлучевой симметрии, но вот двухлучевая симметрия не гарантирует и даже не подразумевает динамической симметрии. Иными словами, двухлучевая симметрия — необходимая, но недостаточная характеристика привлекательного человеческого лица. Объясняет сам Марквардт: «Вы можете нарисовать Альфреда Э. Ноймана[5] с идеальной двухлучевой симметрией, но он от этого не превратится в Пола Ньюмана». Живые, растущие существа динамичны, и именно такая симметрия делает их по-настоящему красивыми.
Доктор Марквардт стал тщательно искать число ?. Божественная пропорция определенно должна быть скрыта в чертах идеального человеческого лица.
Если бы Голливуд снял фильм о докторе Марквардте, то там обязательно была бы сцена, как тот сидит за столом и прикладывает компас и транспортир к фотографиям девушек с обложек журналов, а потом — другая сцена, с кучей затупившихся карандашей на переднем плане, где он выводит сложную формулу с квадратными корнями и алгебраическими переменными. И вот наконец — момент прозрения. Новый кадр: Марквардт поднимает свой шифр и подносит его к камере — лист ацетатной бумаги, на котором жирными черными линиями напечатана «Первичная золотая десятиугольная матрица», угловатая маска, обозначающая идеальное человеческое лицо.
«Маска Марквардта» — это матрица из точек, линий и углов, составляющих геометрический каркас и границы так называемого архетипического лица, построенный граф визуального идеала, к которому стремится наше коллективное бессознательное. Внутри матрицы скрываются сорок две вторичных «золотых десятиугольных матрицы» той же самой формы, что и большая матрица, но меньше в ? или несколько ? раз. С большой матрицей они пересекаются как минимум двумя вершинами‹‹99››. «Маска» определяет идеальное трехмерное расположение каждой черты лица, от размера глаз и расстоянии между ними до ширины носа, полноты верхней и нижней губы и т. д.

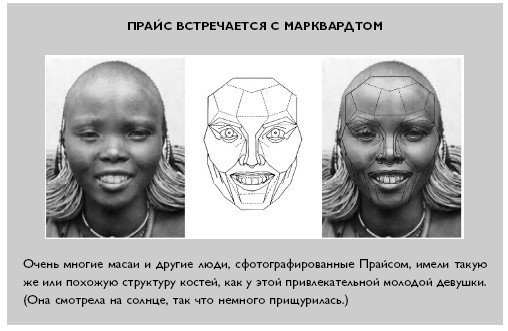
В документальном сериале Джона Клиза The Human Face («Человеческое лицо») на канале ВВС, в котором участвовал Марквардт и использовались его исследования, прозрачный каркас маски накладывали на фотографии Мэрилин Монро, Хэлли Берри и Элизабет Тейлор‹‹100››. Маска подходила ко всем лицам идеально, словно хрустальный башмачок к ножке Золушки, доказывая тем самым, что несмотря на различия в цвете кожи и прическах, эти культовые суперзвезды сложены одинаково пропорционально, а архетипическая маска — вовсе не совпадение. Вот вам и «красота в глазах смотрящего». Красивые люди рождаются не благодаря удаче, а потому, что любая ДНК естественным образом стремится создать динамически симметричную геометрию, стимулируя рост тканей.
В работе Марквардта мы видим вполне конкретную лицевую геометрию, создаваемую здоровой человеческой ДНК. Она продолжает традицию многих архитекторов и математиков, обнаруживших число ? в человеческом теле: Витрувия в I веке до нашей эры (именно этот архитектор вдохновил Да Винчи на создание «Витрувианского человека»); Леона Баттисты Альберти и Франческо ди Джорджо Мартини в XV веке; Луки Пачоли и Себастьяно Серлио в XVI веке; Шарля-Эдуара Жаннере-Гри, более известного как Ле Корбюзье, в XX веке. Адольф Цейзинг, возможно, говорил за всех них, когда в 1854 году заявил, что в золотом сечении «содержится фундаментальный принцип всех форм, стремящихся к красоте и полноте в мире природы и в живописном искусстве, который с самого начала был высшим стремлением и идеалом всех фигур и отношений форм — космических и индивидуальных, органических и неорганических, акустических и оптических, — и который нашел свое идеальнейшее воплощение только в человеческой фигуре»‹‹101››.
Как и египетские ученые, которые тысячи лет назад обнаружили математический порядок на земле и на небе, я верю, что те же математические принципы, что упорядочивают вселенную, управляют и ростом всех частей тела всех живых существ. Когда этот рост идет оптимально, то неизбежным его результатом являются красивые и функциональные биологические структуры. Это не новая идея — она высказывалась еще в трудах древних философов, от Платона до Пифагора. Но сейчас мы можем понять то, чего не могли знать в древности: как именно человеческий мозг так легко проводит столько математических расчетов, мгновенно распознавая сложные геометрические формы и превращая их в эмоции — желание, восторг, спокойствие, страх.






